Uma distribuição de cargas com densidade linear constante está localizada ao longo do eixo no intervalo conforme a figura.
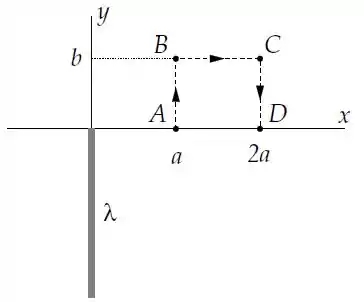
Calcule o vetor campo elétrico num ponto qualquer do eixo com coordenada .
Adotando-se potencial nulo no ponto do eixo com , calcule o potencial elétrico num ponto do eixo com coordenada .
Determine o trabalho que deve ser realizado para levar uma carga do ponto do eixo em ao ponto do eixo em segundo a trajetória mostrada na figura.
Passo 1
Calcule o vetor campo elétrico num ponto qualquer do eixo com coordenada .
A boa aqui é sempre partir de um pedaço infinitesimal de carga pra começar a análise do problema. Esse pedaço infinitesimal de carga vai gerar um campo elétrico , dado por:
Por definição:
Logo:
Graficamente, a ideia é essa:
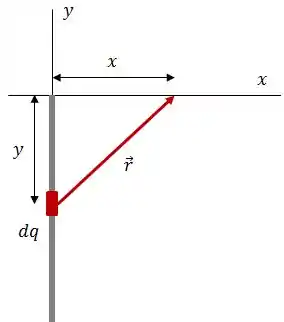
Sendo assim, podemos tirar algumas conclusões aqui:
O vetor é dado pela subtração vetorial do ponto onde queremos calcular o campo com o ponto onde tá a nossa fonte de campo , ou seja
Substituindo isso na expressão para o campo elétrico:
Esse é o momento que você se dá conta das integrais que vai ter que resolver pra acabar o problema, começa a suar frio, a garganta fica seca e tal... eu sei como é a sensação!
Mas relaxa! Essas integrais vivem aparecendo em problemas desse tipo, e a solução delas geralmente já estão até nos formulários, então antes de se desesperar, dá uma olhada lá! É provável que a resposta da integral esteja por lá mesmo.
Passo 2
As integrais são essas daqui:
Substituindo de volta:
Passo 3
Adotando-se potencial nulo no ponto do eixo com , calcule o potencial elétrico num ponto do eixo com coordenada .
A partir da definição de potencial elétrico:
Como estamos analisando o potencial apenas sobreo eixo , . Logo:
Passo 4
Determine o trabalho que deve ser realizado para levar uma carga do ponto do eixo em ao ponto do eixo em segundo a trajetória mostrada na figura.
O trabalho, por definição, independe da trajetória. Então não tem a menor necessidade de você se matar aí fazendo conta, basta calcular o trabalho entre os pontos e .
Onde:
Portanto:
Resposta