Quatro cargas puntiformes são colocadas nos vértices e de um retângulo, de
acordo com a figura abaixo. O retângulo tem lados de comprimento e . Considere
.
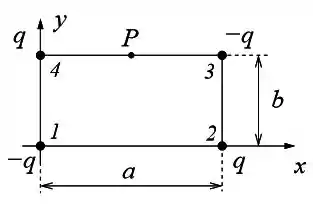
Calcule o vetor força resultante que atua na carga localizada na origem
(vértice ).
Determine o vetor campo elétrico no centro do retângulo ponto de
coordenadas .
Calcule o trabalho necessário para trazer uma carga do infinito até o
ponto de coordenadas .
Passo 1
Como na origem temos a carga , vamos então descobrir a força resultante nessa carga.
E para isso vamos, calcular a força nessa carga gerada pela carga , depois pela e por último pela , separadamente. E então, vamos somar essas forças e calcular a resultante.
Porém, antes podemos fazer uma analise qualitativa do resultado, lembrando que cargas positivas se atraem e cargas negativas se repelem e o módulo da força é inverso ao quadrado da distância devido à fórmula da força:
Assim, teríamos essas forças agindo:
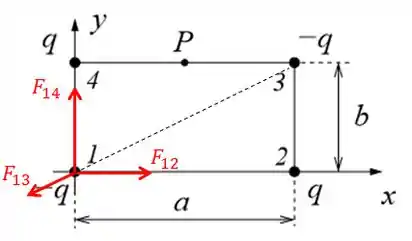
Passo 2
Agora vamos então calcular as forças separadamente.
Primeiro a força entre as cargas e :
Observe que essa força atua apenas na direção do eixo .
Agora, a força entre as cargas e , nesse caso vamos dividir a força em dois vetores o vetor força na direção , onde as cargas distam de , e o vetor força na direção , onde as cargas distam de . Assim, temos:
Onde:
Então podemos achar o valor da força, como:
Por último, vamos calcular a força entre as cargas e
Passo 3
Agora, vamos calcular a força resultante somando as forças
Passo 4
Como as cargas estão postas simetricamente em relação ao ponto pedido, então teremos que o campo elétrico será nulo.
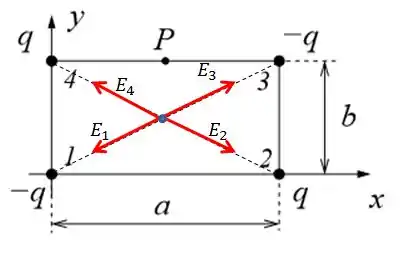
Porque o campo gerado pela carga irá anular o campo gerado pela carga e o mesmo ocorrerá com os campo de e .
Assim, .
Passo 5
Queremos agora calcular o trabalho necessário para trazer uma partícula de carga do infinito ao ponto . Como vimos na teoria, esse trabalho é igual a variação de energia potencial entre o infinito e o ponto , como no infinito consideramos a energia potencial igual a zero. Então:
Para descobrirmos a energia potencial no ponto , vamos somar a energia potencial gerada por cada carga naquele ponto, então: