Densidade de Carga, Lei de Gauss, Potencial Elétrico
Dois semi-planos condutores infinitos se encontram num ângulo reto. Na região entre eles o potencial elétrico é dado por
onde é uma constante positiva.
Determine o campo elétrico no primeiro quadrante .
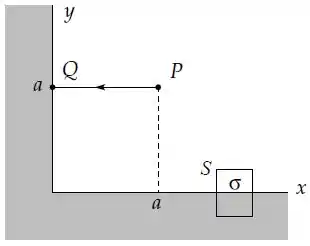
Usando a lei de Gauss com a superfície fechada, cilíndrica e infinitesimal, mostrada de perfil na figura, determine a densidade superficial de carga na face horizontal do condutor.
Determine a integral de linha do campo elétrico
ao longo do segmento de reta , conforme a figura.
Passo 1
Determine o campo elétrico no primeiro quadrante .
Por definição, o campo elétrico e o potencial estão associados por:
Passo 2
Usando a lei de Gauss com a superfície fechada, cilíndrica e infinitesimal, mostrada de perfil na figura, determine a densidade superficial de carga na face horizontal do condutor.
A Lei de Gauss é dada por:
Já que e são paralelos, podemos simplificar a Lei de Gauss para:
Assim, no ponto , teremos:
O campo independe de . Quando , o campo elétrico possui somente a componente . Logo:
Passo 3
Determine a integral de linha do campo elétrico ao longo do segmento de reta , conforme a figura.
O problema está pedindo para calcularmos a integral
Por definição:
Agora ficou fácil!
No ponto , e e no ponto , e . Portanto:
Finalmente:
Resposta