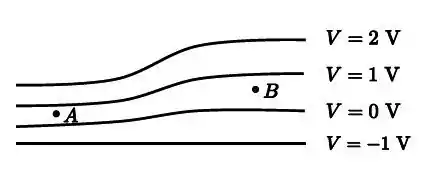
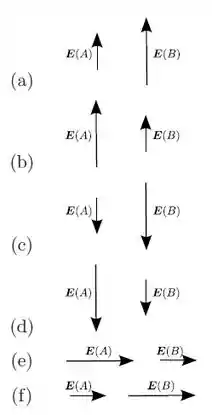
Considere o seguinte corte perpendicular a uma família de quatro superfícies equipotenciais, associadas a um campo eletrostático. Assinale a opção que melhor indica o vetor campo elétrico em cada um dos pontos A e B, respectivamente.

Agora vem a parte difícil... Dois jeitos de fazer. Vamos ver qual você prefere. Podemos tratar com qualquer uma das duas fórmulas:

O que você tem que saber fazer é uma análise qualitativa dessas duas fórmulas.

Vamos pegar a primeira. Fazer uma análise qualitativa significa que você pode chutar algumas particularizações que não comprometam a sua análise. Ou seja, são particularizações genéricas o suficiente (hahahah) pra você conseguir pensar sem estragar o problema. É sério isso. Vamos lá, vai ficar mais claro na prática. Uma boa é nós pegarmos a primeira fórmula e chutarmos que o campo é uniforme. Por conta disso ele vai sair do produto escalar e da integral:

Não tem problema fazer esta particularização porque só queremos uma aproximação. Fazendo a integral para dois caminhos: um passando por e outro passando por , temos:

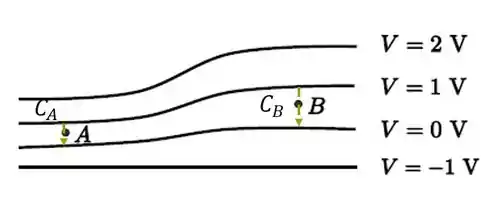
A diferença de potencial nos caminhos é igual.

Temos então:

Entretanto, temos claramente que:

Logo, igualando:

Único jeito dessas coisas serem iguais é:

Fim de papo. Chegamos à resposta já! Mas vamos ver como seria da outra forma...

ALTERNATIVAMENTE, usando a outra fórmula temos:

Que o campo em um ponto é o gradiente do potencial naquele ponto. Como o gradiente são derivadas parciais:

A gambiarra neste caso é aproximar as derivadas com variações discretas. Já vai ficar claro, na real é +/- intuitivo. Como só importa o campo na direção do eixo (finge que tem um eixo lá):

Ou seja, o campo é a razão entre a variação do potencial e a variação da altura entre os dois pontos. Na região de temos uma variação menor, portanto:

Já a variação do potencial é igual pros dois:

Ah, mas e o sinal de menos? Não importa nesse caso pois nós já sabemos que aponta pra baixo e só estamos preocupados com o módulo mesmo.