Um dipolo elétrico é colocado no eixo com em e em .
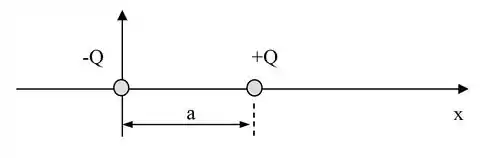
Calcule o potencial elétrico num ponto qualquer do eixo para . Considere o referencial de potencial nulo no infinito.
Apesar do potencial da letra não ser genérico, mesmo assim podemos, a partir dele, encontrar uma componente do campo elétrico. Responda qual é esta componente e calcule-a.
Se uma carga pontual for colocada no ponto , calcule a força elétrica sobre ela e a energia potencial associada à configuração.
Passo 1
Como queremos o potencial apenas sobre o eixo , as coisas ficam um pouco mais simples, vamos começar lembrando do potencial gerado por uma carga:
Onde é a constante eletrostática, é o valor da carga em questão e é a distância da carga ao ponto.
Para qualquer ponto do eixo , onde , temos que a carga negativa irá produzir um potencial:
Analogamente, a carga positiva, irá produzir um potencial:
Sabendo que o potencial obedece ao princípio da superposição, temos que o potencial em qualquer ponto do eixo , sendo , vale:
Passo 2
Como temos a função do potencial somente em função de , só poderemos calcular a componente do campo elétrico. Para isso, vamos lembrar da seguinte relação entre campo elétrico e potencial:
Como podemos calcular somente a componente , temos:
Passo 3
Para determinar a força que atua na carga, basta lembrar que:
No caso, temos:
Para determinar a energia da configuração, precisamos lembrar que:
No caso, temos:
Resposta
;