Considere um dipolo elétrico formado por duas cargas de módulo e com sinais opostos, separadas por uma distância . O módulo da posição radial a uma ponto genérico , definida em relação à origem localizada no centro do dipolo, é dado por , que, por sua vez, define o ângulo em relação ao eixo do dipolo (veja figura abaixo).
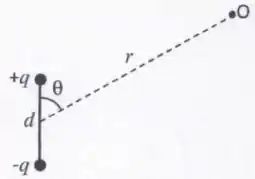
- Num ponto para o qual , calcule o potencial elétrico gerado pelo dipolo em função de e do momento de dipolo .
- A partir do resultado do item a), calcule a componente radial do vetor campo elétrico gerado pelo dipolo no ponto .
- Para uma distância , em que regiões do espaço a componente radial do campo elétrico atinge valores máximos? Discuta seu resultado usando o conceito de linhas de campo elétrico.
Passo 1
a) Para o cálculo do potencial, vamos considerar as figuras abaixo.
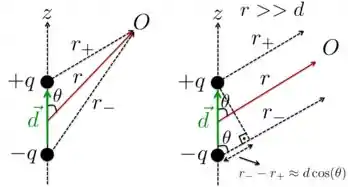
O potencial no ponto O será dado pela soma dos potenciais produzidos pelas cargas nesse ponto. Portanto,
Quando no caso em que e são praticamente paralelos, como mostra a figura acima para , e podemos fazer as seguintes aproximações:
Substituindo na expressão para o potencial no ponto , , chegamos a:
Passo 2
b) Sabemos que o . Portanto, tomando a expressão que acabamos de encontrar para o potencial , temos que
Passo 3
c) Para fixa, será máximo se , ou seja, se ou . Assim, os valores máximos de ocorrem nos pontos localizados sobre o eixo , que o eixo do dipolo.
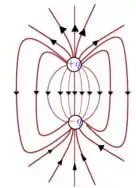
Isto é razoável à luz do diagrama de linhas de campo de um dipolo elétrico, no qual se percebe um nítido adensamento das linhas sobre o eixo .
Resposta
- Para fixa, será máximo se , ou seja, se ou .