Seja uma função contínua satisfazendo as seguintes propriedades:
- e
- é derivável até segunda ordem em ;
- Existe uma função contínua tal que para todo e
- Existe uma função contínua tal que para todo e
(a) Usando a Regra de L’Hospital para calcular o limite, decida se é derivável em e determine, em caso afirmativo, .
(b) Estude f em relação a seus intervalos de crescimento e decrescimento, intervalos de concavidade, pontos de máximo e mínimo locais e globais e pontos de inflexão.
(c) Esboce o gráfico de .
Passo 1
Fala aí galerinha? Tudo bem com vocês? Bora resolver essa questão! No item a) ele pede pra gente usar o L’Hospital pra calcular o limite. Mas vocês lembram a hipótese fundamental para que possamos usar esse artifício? Precisamos que seja contínua no ponto em que o limite tende. Como a primeira afirmativa da questão é que , isso significa que ela é contínua em 0 e a gente pode aplicar L’Hospital tranquilamente. Sabendo disso, bora lá pela definição de L’Hospital:
Desenvolvendo:
Agora aplicamos L’Hospital, derivando numerador e denominador. Dessa forma:
Mas pera aí, quem é mesmo? A questão nos deu! Temos que:
Logo:
Ao aplicarmos o valor do limite, o denominador tende a (e é estritamente positivo). O numerador por sua vez tende a . Portanto, o nosso limite é igual a:
Logo não é derivável em (pois o limite não converge e vai pra ).
E é isso, bora pro item b)?

Passo 2
Aqui no item b) a questão pede pra gente estudar essa função em vários aspectos. Bora lá separar e entender cada um deles. Começamos estudando primeiro as raízes do polinômio da função .
Vamos ao teste de pontos críticos? (Esse teste vai nos dizer aonde a função cresce e decresce). No numerador, a única raíz pra esse polinômio é . Sabemos disso ao calcularmos:
Como é estritamente positivo se , temos que como único ponto crítico. Portanto, para valores menores que ele nossa função recebe valores , e em valores maiores que nossa função é positiva (para todo ), logo:
se
se ou
Passo 3
Passo 4
Ainda no item b), como é contínua, significa que ela não tem descontinuidades (fala sério?!) Mas calma, dizer que não tem descontinuidades significa dizer que o nosso ponto de inflexão dita aonde a função é crescente (derivada da função no intervalo é positiva) e decrescente (derivada da função no intervalo é negativa). Como o nosso ponto crítico é , logo nossa função é:
Passo 5
Pra gente matar o item , vamos atras das concavidades da função. Pra acharmos essas concavidades precisamos da derivada segunda da função. Se a primeira derivada nos diz pontos críticos da função, a derivada segunda nos diz sobre concavidades e pontos de inflexão. E o melhor de tudo é que a questão já nos deu a derivada segunda da função. Saca só:
Semelhantemente ao passo 2, vamos analisar essa função no numerador e denominador. No numerador temos essa parábola:
Procurando as raízes dela:
As raízes reais para esse polinômio são:
Para o denominador, a única raiz é:
E esses pontos são justamente pontos de inflexão (mas jaja te conto mais sobre isso). Como temos 3 pontos de inflexão, a função tem 4 mudanças de concavidade (sempre a quantidade de pontos de inflexão + 1). E essas mudanças de concavidade (pelo sinal das raízes) vão acontecer justamente em: Para concavidades para baixo:
Concavidade para cima:
Substituindo: Para concavidades para baixo:
Concavidade para cima:
Passo 6
E por fim, para desenharmos um esboço da função, vamos reunir todas as infos que a gente tem:
Concavidades:
Para concavidades para baixo:
Concavidade para cima:
Ângulo da função:
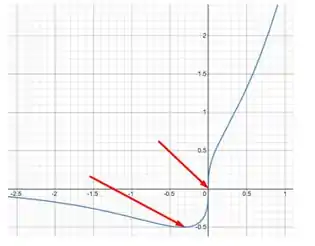
Então o gráfico da função é algo como:
Resposta
a)