O abastecimento de água de um prédio é feito por uma tubulação, conforme o esquema a figura abaixo. Após passar por canos de seção reta e , a água segue por um cano de seção reta até sair( ponto 4) para a caixa d’água localizada no alto do edifício. Entre as posições 1 e 2 na tubulação é colocado um manômetro que mede a diferença de pressão . A altura do prédio é e o volume da caixa d’água é
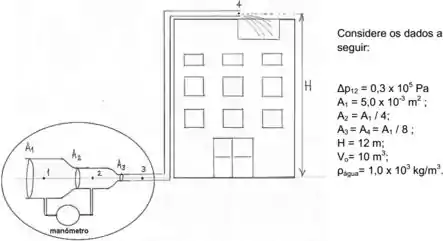
- Encontre a velocidade , no ponto 1 do encanamento.
- Determine a vazão no tubo e o tempo necessário pra encher a caixa d’água.
- Determine a velocidade , com que a água sai pela extremidade do tubo no alto do edifício.
- Determine a pressão manométrica no ponto 1(, que foi necessária para fornecer a vazão calculada.
Passo 1
a):
Pra resolver esse item a gente vai usar Bernoulli.
Bom, temos a diferença de pressão entre os dois pontos. Só que não sabemos a velocidade do fluido em nenhum ponto. A relação das pressões e velocidades nos pontos 1 e 2 por Bernoulli é dada por:
Então:
Mas ainda temos mais variáveis que equações. Mas olha só, a velocidade 1 se relaciona com a velocidade 2 a partir do princípio da continuidade, não é?
Isso é, como a vazão da bomba é a mesma nos dois pontos, a gente pode escrever essa parada assim:
Então:
Nós sabemos o valor de . Então:
Passo 2
b):
Pra determinar a vazão basta a gente usar aquela fórmula:
E o tempo que leva pra encher a caixa é calculado pela divisão e por esse valor:
Passo 3
c):
Pra descobrir isso, basta a gente perceber que o cano que libera a água no ponto 4 é o mesmo que sai lá de baixo e tem seção transversal Assim:
Passo 4
d):
Vamos usar a equação de Bernouli entre os pontos 1 e 4 pra achar a pressão manométrica .
Isso porque a pressão em 4 é a pressão atmosférica. Então:
Então:
Resposta
a):
b):
c):
d):