Um fluido ideal de densidade , escoa através de um tubo horizontal com regiões 1 e 2, conforme ilustra a figura ao lado. Quando o fluido está na região 1, ele tem velocidade v1 = 0,20 m/s e pressão Pa. Sabendo que o diâmetro na região 2 é um quarto do diâmetro do tubo na região 1, responda às perguntas abaixo.
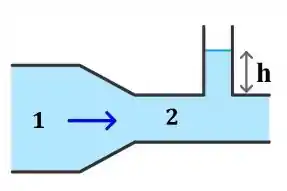
(a) Qual é a velocidade do fluido que atravessa a região 2?
(b) Qual é a pressão interna no cano da região 2?
(c) Se na região 2 há um tubo vertical com abertura para a atmosfera, qual é a altura h da coluna de fluido formada nessa abertura?
Passo 1
a) Pra calcular essa velocidade aí vamos usar a equação da continuidade:
Substituindo:
Passo 2
b) Vamos ter que aplicar Bernoulli!
A altura das duas regiões é a mesma! Então a gente pode cancelar essas parcelas com e com . Para os outros caras:
Substituindo everybody, temos:
Passo 3
c) A pressão no ponto 2 vai ser igual à pressão devida à coluna de fluido mais a pressão atmosférica. Então:
Resposta
a)
b)
c)