Equação da Continuidade, Equação de Bernoulli
Um reservatório cilíndrico circular de diâmetro contém um combustível líquido com densidade , suposto ideal, Esse reservatório possui uma tampa pesada, de massa , que pode se mover verticalmente, em m contato permanente com o fluido e exercendo pressão sobre sua superfície. Acima da tampa existe ar à pressão atmosférica. Na região lateral desse reservatório, mais abaixo, há uma abertura com uma válvula conectada a um tubo horizontal de diâmetro , para escoar o fluido. A válvula é aberta quando a distância vertical entre a superfície do líquido e o centro do tubo é de . Considere .
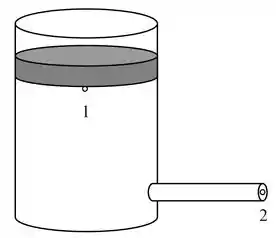
Calcule a velocidade do fluido no tubo horizontal.
Determine a vazão e a velocidade de descida da tampa.
Coloca-se, na extremidade do tudo, um bico com diâmetro de saída igual à metade do diâmetro do tubo. Determine a nova vazão e a pressão manométrica no centro do tubo.
Passo 1
Para calcular a velocidade do fluido no tubo horizontal, vamos utilizar a equação de Bernoulli, iremos utilizar os pontos e que estão destacados na figura! Se liga
Substituindo os valores dados, temos:
Repare que no ponto , a pressão é a soma da pressão atmosférica com a pressão exercida pela tampa. Além disso estou considerando e por conta disso, .
Sabemos, que para um escoamento incompressível, temos a seguinte relação:
Substituindo na equação de Bernoulli, temos:
Passo 2
Para calcular a vazão, podemos utilizar qualquer ponto, pois por se tratar de um líquido incompressível, a vazão será sempre a mesma. Como já temos a velocidade no ponto , iremos utilizar esse ponto para achar a vazão.
A velocidade de descida tampa será a mesma velocidade de escoamento do líquido no ponto , pela relação entre e que já tínhamos achado, temos:
Passo 3
Pela equação de Bernoulli, podemos perceber que a velocidade no tubo horizontal não depende do diâmetro do tubo, e sim da sua altura, portanto, a velocidade no bico continua a mesma do tubo . Portanto, a nova vazão será:
Para determinar a pressão manométrica no centro do tubo, vamos, mais uma vez, utilizar a equação de Bernoulli, só que agora entre, um ponto no tubo e um ponto no bico:
Podemos determinar a nova velocidade pela seguinte relação:
Substituindo na equação de Bernoulli, temos:
Como é pedida a pressão manométrica, tivemos que subtrair a pressão atmosférica .
Resposta
;
;