Na figura abaixo, a água escoa suavemente pela tubulação descendo uma altura do ponto 1 ao ponto 4. Os pontos 1 e 2 estão na mesma altura, assim como os pontos 3 e 4. A área da seção reta no ponto 1 é . As áreas das seções retas dos tubo em 4,3 e 2 têm a relação:
Mede-se a diferença de pressão entre os pontos 4 e 1 e obtém-se . Considere ,
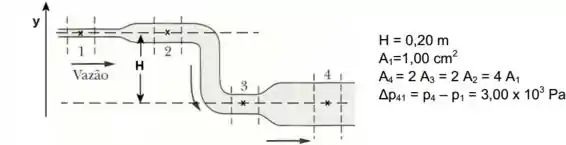
- Determine a expressão para a velocidade de escoamento no ponto 1, , em função de , , e . Calcule essa velocidade
- Determine a diferença de pressão entre os pontos 3 e 4, .
- Calcule a velocidade do nível da água na caixa quando as vazões nos apartamentos são e respectivamente. ( Dê a resposta em e ).
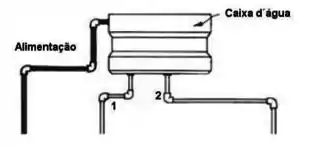
A figura representa uma caixa d’água alimentada com água bombeada à razão de litros por minuto. A superfície livre de água na caixa tem área . Dois canos( 1 e 2) distribuem a água a dois apartamentos.
Passo 1
a), bom, como era de se esperar, vamos usar a equação de Bernoulli nessa questão.
Além disso, vamos usar a equação da continuidade. Vamos deixar essa parte pronta loga pra depois substituirmos:
Sacou? Deixamos em função de pra gente substituir no fim. Afinal, queremos descobrir o . Então:
Usamos o nível zero como o nível onde estão os pontos 3 e 4. Então:
Passo 2
b):
Como os pontos estão a mesma altura, aplicar Bernoulli fica fácil:
Então:
Pela equação da continuidade:
Só que quanto vale ? Lembrando de a) que:
Então:
E:
Passo 3
c):
Bom, primeira coisa que vamos descobrir aqui é a taxa com o qual o volume varia. Isso é um pouco de cálculo 1, se você fizer uma força pra lembrar.
Temos ali uma fonte que fornece volume à caixa d’água, e duas fontes que retiram volume. Então a taxa total é dada por:
Show!
Agora é muito simples, temos a vazão e a área, pra descobrir a velocidade com que o nível da água varia, basta aplicar a definição de vazão:
Mas antes vamos ter que fazer umas conversões.
Lembrando que um litro tem
E :
Mas também podemos escrever ( só substituindo o valor de um litro):
Resposta
a):
b):
c):