Um fluido incompressível flui da esquerda para a direita por uma tubulação de seção reta circular com diâmetro variável. A figura mostra apenas um pedaço da tubulação, que sai para a atmosfera no ponto . A densidade do fluido é de e os diâmetros das seções transversais em e em são iguais a e , respectivamente. O ponto está acima do ponto . Deseja-se uma vazão de saída de .
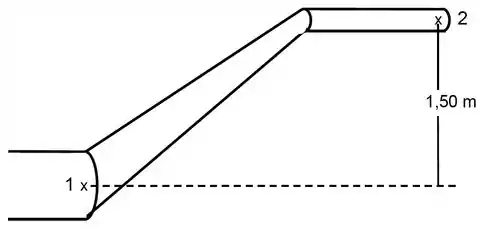
Determine quais devem ser as velocidades de escoamento no ponto , , e no ponto ,
Determine a pressão manométrica a que deve estar submetido o fluido no ponto para que se obtenha a vazão desejada.
Calcule a potência necessária para fornecer essa vazão.
Passo 1
Para determinar as velocidades de escoamento, iremos usar a definição de vazão em volume, já que foi dado no enunciado a vazão no ponto :
Onde é a área da seção e , a velocidade!
Do enunciado, temos:
Substituindo na equação:
Pela equação da continuidade. Temos:
Passo 2
Para determinar a pressão manométrica a que deve ser submetido o líquido, devemos utilizar a equação de Bernoulli:
Vamos agora reunir os dados que temos para substituir nessa equação:
Agora é só calcular a pressão manométrica, lembrando que ela é dada por:
Agora é só substituir na equação:
Passo 3
Para determinar a potência necessária, precisamos lembrar que ela pode ser definida da seguinte maneira:
Lembrando que pressão e força se relacionam da seguinte maneira:
Temos:
Substituindo, temos:
Resposta
,