Um fluido incompressível escoa suavemente (fluxo ideal) da esquerda para a direita pela tubulação da figura ao lado. Considerando como a vazão, como a velocidade e como a pressão do fluido, marque a resposta correta em relação às regiões 1 e 2 ilustradas na figura.
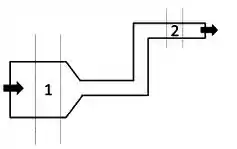
a) , ,
b) , ,
d) , ,
e) , ,
f) , ,
g) , ,
h) , ,
i) , ,
j) , ,
Passo 1
Ele disse que a vazão é . Pela equação da continuidade, sabemos que:
Show! Já matamos descartamos algumas alternativas.
A equação da continuidade nos dias também que:
Como pela figura:
Então:
Passo 2
Vamos aplicar Bernoulli entre os dois pontos. E vou tomar o ponto 1 como referencial, de forma que .
Se o lado direito da equação for maior que zero, .
Como e :
Resposta
Letra H.
Exercícios de Livros Relacionados
O tubo de Pitot (veja a figura) é usado para medir a velocidade do ar nos aviões. Ele é formado por um tubo externo com pequenos furos B (quatro são mostrados na figura) que permitem a entrada de ar n
Na figura, a água entra em regime laminar no lado esquerdo de uma tubulação (raio r 1 = 2,00R ), atravessa a parte seção central (raio R ), e sai pelo lado direito (raio r 3 = 3,00R ). A velocidade da
As linhas de correntes horizontais em torno das asas de um pequeno avião são tais que a velocidade sobre a superfície superior é igual a 70,0m/s e sobre a superfície inferior é igual a 60,0m/s. Se a á
A figura mostra um jorro d’água saindo por um furo a uma distância h = 10c m da superfície de tanque que contém H = 40c m de água. (a) A que distância x a água atinge o solo? (b) A que profundidade de
A água se move com uma velocidade de 5,0m / s em um cano com uma área de seção reta de 4,0c m 2 . A água desce gradualmente 10 m enquanto a seção reta aumenta para 8,0c m 2 . (a) Qual é a velocidade d