Água flui da esquerda para a direita através do tubo horizontal mostrado na figura a seguir. No ponto , a área da seção reta vale e a velocidade da água é . No ponto a área vale . Nos tubos verticais que estão em contato com o horizontal a água está em repouso e em contato com a atmosfera nas suas extremidades superiores. A altura da coluna vertical de água no interior do tubo do lado direito é de enquanto a do lado esquerdo, , será determinada a seguir. Considere que a densidade da água vale Considere .
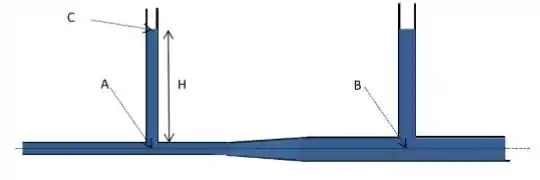
Qual a velocidade da água no ponto , em ?
A pressão no ponto se relaciona com a no ponto C de acordo com
Quanto vale, em , a altura ?
Passo 1
Pelo principio da continuidade temos que
Assim,
Encontramos a velocidade no ponto
Como a área aumentou de para , para a vazão continuar a mesma a velocidade tem que diminuir e é essi que acontece, ela cai de para .
Alternativa
Passo 2
Pelo principio de Stevin, a pressão em será a pressão em mais a pressão da altura de líquido.
Assim,
O que nos mostra que a alternativa correta é a
Passo 3
No Passo relacionamos a altura com a pressão e , é a pressão atmosférica, então precisamos descobrir apenas a pressão em , para conseguirmos calcular a altura .
Mas para encontramos , primeiro temos que encontrar , então para encontrar essa pressão vamos usar a informação dada no enunciado que a altura da coluna de liquido acima de é de .
Assim, pelo principio de Stevin a pressão em é a pressão atmosférica mais a pressão da altura da coluna de líquido.
Agora que descobrimos a pressão em , podemos, pela equação de Bernoulli, achar a pressão em .
Levando em conta que os pontos e estão na mesma altura, e temos as velocidade em cada ponto.
No passo anterior vimos que a pressão em e em se relacionam da seguinte forma
Então:
Desta forma a altura é aproximadamente
Chegamos assim na alternativa como a correta.