Água flui da esquerda para a direita através do tubo horizontal mostrado na Figura a seguir. No ponto A , a área da seção reta vale 4,00 cm2 e a velocidade da água é VA =6,00 m/s. No ponto B a área vale 10,0 cm2 . Nos tubos verticais que estão em contato com o horizontal a água está em repouso e em contato com a atmosfera nas suas extremidades superiores. A altura da coluna vertical de água no interior do tubo do lado direito é de 200 cm enquanto a do lado esquerdo, H , será determinada a seguir. Seja ρ a a densidade da água. Considere g=10,0 m/s 2 . Responda as questões 5 e 6.
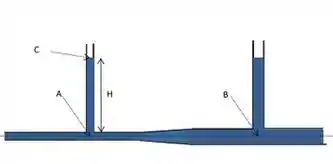
Quanto vale, em cm, a altura H?
A) 31
B) 49
C) 80
D) 231
E) 249
Passo 1
Vamos aplicar Bernoulli entre os pontos A e B! Então:
As alturas e são iguais. Então podemos cortar dos dois lados:
Passo 2
Vamos achar as pressões .
Com h conhecido e igual a 2 m.
Vamos substituir esses caras lá em Bernoulli:
O único carinha que nós não temos aí nessa equação é o né? Mas podemos descobrir, usando a continuidade:
Substituindo:
Repare que aqui eu não precisei transformar a área pra metro quadrado, porque é a mesma unidade dos dois lados, com o mesmo fator de conversão, não faz diferença.
Passo 3
Vamos substituir tudo que a gente tem lá em Bernoulli!
Resposta
Letra B.