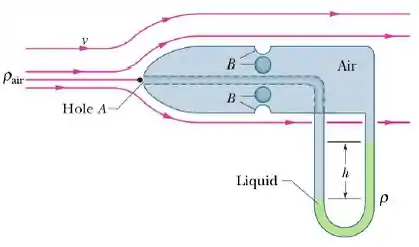
A figura abaixo mostra um esquema de um tubo de Pitot, que é usado para medir a velocidade do ar nos aviões. Ele é formado por um tubo externo com pequenos furos B (quatro são mostrados na figura) que permitem a entrada de ar no tubo; este tubo está ligado a um dos lados de um tubo em de U. O outro lado do tubo em forma de U está ligado ao furo A na frente do medidor, que aponta no sentido do movimento do avião. Em A o ar fica estagnado, de modo que . Em B, porém, a velocidade do ar é presumivelmente igual à velocidade do ar em relação ao avião. Considere a diferença de altura entre A e B desprezível.
a) Seja ρ a massa específica do líquido contido no tubo em U e h a diferença entre os níveis do líquido no tubo.Sendo a densidade do ar , encontre a expressão que determina a velocidade do avião.
b) Suponha que o tubo contém um liquido cuja massa específica é e que a diferença de nível medida é 40,0 cm. Qual é a velocidade do avião em relação ao ar? A massa específica do ar é .
Passo 1
a) Aqui a gente vai ter que aplicar Bernoulli entre os dois pontos.
Vamos considerar que eles estão na mesma horizontal, então .
Além disso, a velocidade no ponto A é zero. Então:
Passo 2
Show! Agora repara comigo que a diferença de pressão entre os pontos A e B é justamente aquela pressão devido à diferença de altura h no tubo. Ou seja:
Então, igualando ao que a gente achou antes:
Passo 3
b) Agora vamos trocar os valores:
Resposta
a)
b)