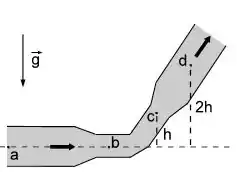
O esquema ao lado mostra a vista lateral de uma tubulação na qual água flui idealmente no sentido indicado. No ponto , a velocidade é e a pressão é . A área da seção transversal da tubulação nos pontos e é um terço da área da seção transversal em e . Considere e .
Calcule a velocidade do fluido nos pontos e .
Calcule a pressão nos pontos e . Em qual desses pontos a pressão é menor? Explique sua resposta.
Passo 1
Estudamos duas matérias que envolviam a velocidade das partículas de um fluido. O principio da continuidade que relaciona a área de cada secção do tubo com a velocidade e a equação de Bernoulli.
Bem, vamos usar um deles para resolver essa questão, visto que queremos a velocidade da partícula em alguns pontos do tubo.
Como o enunciado nos forneceu a seguinte relação: “A área da seção transversal da tubulação nos pontos e é um terço da área da seção transversal em e .”
Conseguimos resolver esse item apenas com o principio da continuidade, pois ele diz que
Além disso temos a velocidade em e a área e ainda temos as relações entres a área com as áreas em .
Assim, já descobrimos que:
Além disso, com a relação:
Temos que:
Agora falta so substituir os valores:
Passo 2
Agora a matéria que relaciona velocidade com pressão é a equação de Bernoulli, então vamos usá-la para resolver a questão. A equação nos diz que:
Sendo que temos que as alturas em cada ponto são:
E ainda , temos a pressão em , , assim podemos jogar esses valores na equação e obter as pressões em cada ponto.
Começando por
Agora que temos vamos encontrar
E por último
Agora podemos dizer que o local com menor pressão é o ponto , por tem uma alta velocidade e uma certa altura a sua pressão cai muito.
Resposta