Em um grande reservatório de água, a entrada da tubulação (veja na figura) tem uma seção reta de e a velocidade da água é . A água desce gradualmente pelo tubo e na saída, a uma profundidade abaixo da entrada, a seção reta é vezes menor.
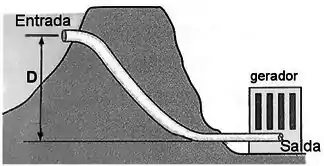
(a) Calcule a velocidade da água na saída.
(b) Calcule a diferença de pressão entre a entrada e a saída
Passo 1
Aqui fazemos a conservação da vazão da água
Pelo enunciado, temos que . Assim
Passo 2
Pela equação de Bernoulli, temos
Onde já setamos a altura na saída como . Assim
(onde usamos a densidade da água e
Resposta
(a)
(b)
Exercícios de Livros Relacionados
O tubo de Pitot (veja a figura) é usado para medir a velocidade do ar nos aviões. Ele é formado por um tubo externo com pequenos furos B (quatro são mostrados na figura) que permitem a entrada de ar n
Na figura, a água entra em regime laminar no lado esquerdo de uma tubulação (raio r 1 = 2,00R ), atravessa a parte seção central (raio R ), e sai pelo lado direito (raio r 3 = 3,00R ). A velocidade da
As linhas de correntes horizontais em torno das asas de um pequeno avião são tais que a velocidade sobre a superfície superior é igual a 70,0m/s e sobre a superfície inferior é igual a 60,0m/s. Se a á
A figura mostra um jorro d’água saindo por um furo a uma distância h = 10c m da superfície de tanque que contém H = 40c m de água. (a) A que distância x a água atinge o solo? (b) A que profundidade de
A água se move com uma velocidade de 5,0m / s em um cano com uma área de seção reta de 4,0c m 2 . A água desce gradualmente 10 m enquanto a seção reta aumenta para 8,0c m 2 . (a) Qual é a velocidade d