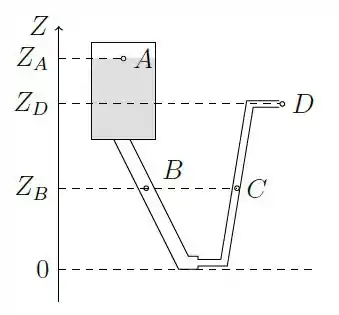
A figura abaixo mostra uma caixa d’água numa certa altura ligada a uma tubulação que desce e depois sobe, tendo sua seção reta reduzida no ponto mais baixo. O nível da água na caixa (ponto ) está a uma altura . A altura da extremidade do tubo (ponto ) está a uma altura . Os pontos e estão a mesma altura . Considere as seguintes situações:
(I) – A extremidade está vedada com uma tampa
(II) – A extremidade está totalmente aberta para a atmosfera.
Comparando a pressão no ponto com a pressão no ponto em cada caso, podemos afirmar que:
(a) Tanto na situação I como na situação II,
(b) Tanto na situação I como na situação II,
(c) Na situação I, , na situação II,
(d) Na situação I, , na situação II,
(e) Na situação I, , na situação II,
Passo 1
Na situação I, o fluido está parado já que tem uma tampa na extremidade . Assim na equação de Bernoulli temos que e, como os dois pontos estão na mesma altura, . Ficamos com a seguinte a equação:
Passo 2
Já na situação II, o fluido está se movendo! A equação de Bernoulli fica então
Tá, mas o que a gente pode fazer com isso aí?
Passo 3
Pra relacionar as velocidades e podemos usar a equação da continuidade!
Pelo enunciado e pela figura vemos que , ou seja
Isso faz com que o lado direito da nossa última equação do passo 2 seja positivo! Assim
Com isso tudo, vemos que a opção correta é a letra d!
Resposta
(d)