A figura abaixo mostra as linhas de corrente de um escoamento em regime estacionário de um fluido através da tubulação cilíndrica de seção reta de área constante.
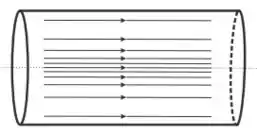
Baseado na figura, considere as seguintes afirmações:
- Uma vez que as linhas de corrente estão mais concentradas na região central do cilindro, a pressão deve ser mínima próxima a região lateral da tubulação.
-A equação de Bernoulli é válida entre quaisquer dois pontos da tubulação.
-A velocidade de escoamento do fluido é maior para as camadas do fluido mais próximas do eixo central do cilindro do que para as mais próximas à superfície lateral da tubulação.
São verdadeiras as afirmativas:
- Somente
- Somente
- Somente
- Somente
- Somente
- Todas são verdadeiras.
Passo 1
Vamos analisar cada um:
- Bom, quando se fala de pressão e velocidade, você deve pensar logo em Bernoulli, já que é essa a equação que relaciona essas grandezas:
Beleza? Bom, vamos considerar que . Nesse caso:
Show? Beleza. Pela essa equação, você consegue ver que, pra manter a igualdade, ao se aumentar a velocidade, se reduz a pressão e vice-versa.
Como no meio a velocidade é maior que nas bordas, vai ser ali que a pressão será menor. A pressão será menor no meio, e não próximo à superfície lateral.:
Falsa.
Passo 2
- Falsa: Por que? Bom, a resposta envolve energia...e viscosidade.
Com as linhas são mais concentradas no centro do tubo e menos concentradas próximas à lateral, no centro a velocidade é maior do que na lateral. Isso quer dizer que há alguma coisa atrasando às moléculas: A viscosidade.
No entanto, a viscosidade é uma força dissipativa. E a equação de Bernoulli é uma forma de equação de conservação da energia.
Só que você deve lembrar que quando há forças dissipativas num sistema, nós não podemos usar conservação da energia ( Isso vem de Fisica1).
Sacou? Não podemos usar Bernoulli em todo o escoamento por causa da presença da viscosidade.
Passo 3
- Verdadeira: Onde as linhas de corrente são mais concentradas existe sempre uma velocidade maior.
Resposta
c)