A figura mostra um esquema de captação de água para uma usina hidrelétrica. Mais à direita, um detalhe da saída do tubo no gerador quando a água já passou pela turbina. Sabendo que a diferença de pressão , que , , e determine (respostas com 3 algarismos significativos e em notação científica):
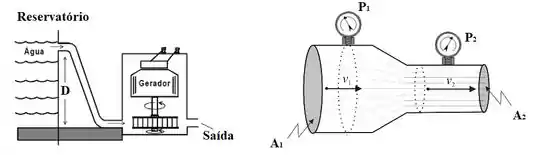
- A velocidade de escoamento
- Considere agora que a altura do espelho de água do reservatório em relação a entrada do tubo seja constante ao longo de um dia. Determine o volume total escoado pela usina em horas
- Determine a profundidade do tubo de entrada de água em relação a superfície de água no reservatório quando não há escoamento de água pela tubulação da turbina. Neste regime, a pressão na altura do tubo de entrada vale
Passo 1
Fala pessoal, tudo certo? Vamos começar? Olha só, nossa questão quer antes de mais nada a velocidade de escoamento da água imediatamente depois de sair do gerador, isto é, . Então bora pensar, qual equação eu posso usar que relaciona a velocidade de escoamento com dados que eu sei? Que tal tentar Bernoulli?
Parece uma boa né? Até porque a velocidade aparece na fórmula! Escolhendo então esses marcos como ponto e :
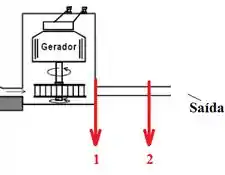
Estamos na verdade escolhendo esses dois pontos:
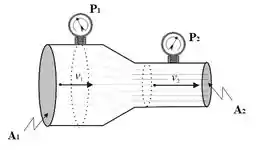
Show de bola, eu tenho informações sobre eles em! Vamos simplificar Bernoulli agora. Pra início de conversa, vamos ter que , já que é uma constante e a gente não mudou de altura entre um ponto e o outro. A equação simplifica então para:
Reorganizando:
Agora, olha só uma coisa importante, apesar da velocidade mudar de um ponto pro outro, a vazão volumétrica não muda! Então:
Como as seções transversais são circulares, podemos escrever essas áreas como áreas de um círculo:
E como o raio é metade do diâmetro:
E opa, ó só! A relação é dado do enunciado! Colocando ela ai:
Por fim, juntando e :
Letra resolvida galera, porque a diferença de pressão é dado do enunciado e a densidade é uma propriedade da água. Seja então, no :
A velocidade, também no , será:
Passo 2
A próxima letra quer da gente um volume total. E inclusive, a questão nos dá uma informação valiosa: “a altura do espelho de água do reservatório em relação a entrada do tubo é constante ao longo de um dia”. Galera, isso é importante porque na entrada do tubo:
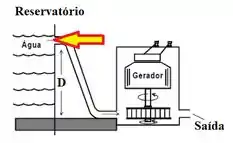
A pressão vai ser a da coluna de água somada a atmosférica. Se a altura do espelho de água não muda, a coluna de água continua constante e logo, a pressão sobre esse ponto também! E se a pressão não variou ao longo do dia, a vazão volumétrica também não! Portanto, seja:
Como o tempo é de , temos:
Como estamos numa parte do problema o diâmetro do tubo não diminui ainda, temos:
Do enunciado e da letra , tiramos:
Tudo no galera, só substituir então:
Passo 3
Mais uma letra e a gente parte pro abraço, viu? A questão quer saber a profundidade do tubo em relação a superfície da água. La na letra a gente não conversou sobre a pessão de entrada ser a atmosférica mais a da coluna d’água? Então, seja o tamanho da coluna de água e, logo, também a profundidade relativa do tubo, temos:
Show galera, é só substituir agora! Afinal o enunciado deu pra gente e o resto a gente sabe! Vamos ter:
Convertendo a pressão lá em cima pra Pascal, ficamos com tudo no e a resposta já sai em metros: