Num túnel de vento para testes aerodinâmicos um fluxo estacionário de ar é estabelecido em torno de um protótipo de asa delgado. O formato da asa é tal que a razão entre a velocidade do ar na parte superior, , e sua velocidade na parte inferior, , vale . Sendo a área da asa, a sua massa, e considerando o ar um fluido incompressível ideal de densidade , a velocidade mínima para que a asa seja sustentada por este fluxo de ar vale:
Passo 1
Essa é uma questão típica, onde aplicamos os conceitos de Bernoulli, então temos que:
Isso, considerando que os dois pontos estão, aproximadamente, à mesma altura. Temos que lembrar, também, da relação da pressão com a força:
Ou seja, pressão é a força dividida pela área de aplicação dessa força.
Para que o avião se estabilize, o formato da asa deve ser tal que a velocidade na parte superior deve ser maior que na parte inferior, à fim de que provenha de uma força de sentido contrário a força proveniente de .
A força que vem de é justamente a força peso dessa asa:
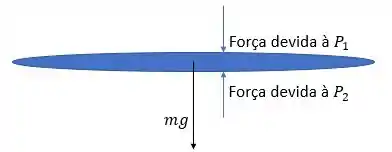
Então, eu sei que esse desenho é ruim rs. Mas foi só para dar uma ideia do que eu estou falando, beleza? Finge que isso em azul é a asa kk.
Agora, você concorda comigo que essa diferença de pressão vai gerar uma força?? Isso porque a pressão, como vimos está relacionada a uma força. Logo, a diferença das pressões vai resultar em uma força também!
Beleza. Para que a asa fique sustentado no ar, isso é parada, a força devida a essa diferença de pressões deve ser igual à força peso que estamos vendo ali também. Ou seja, se é a força devida à e é a força devida à , temos que . Com isso, queremos que:
Logo, na nossa equação:
Substituindo a relação que encontramos das pressões:
Dando uma arrumada:
Como o enunciado nos diz que :
Isolando :
Resposta
Letra a