De uma barragem parte uma canalização de diâmetro interno , com poucos metros de extensão, havendo depois uma redução para . Do tubo de diâmetro , a água passa para a atmosfera sob a forma de um jato. A vazão foi medida, encontrando-se 100 L/s. Considerando o escoamento ideal, calcule:
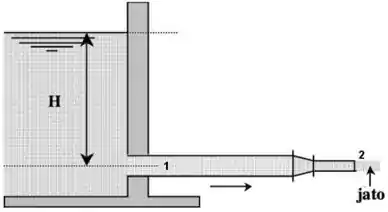
a) a pressão manométrica na parte inicial do tubo de diâmetro .
b) a altura H de água na barragem.
c) a densidade de energia cinética transportada pelo jato e a potência do jato (energia por unidade de tempo).
Passo 1
Questão de hidrodinâmica já lembra logo que só tem duas fórmulas! O princípio da continuidade:
Onde R é a vazão de líquido (volume/tempo), A é a área da seção reta e v a velocidade do líquido naquea região.
E a equação de Bernoulli:
Ambas são sempre usadas para comparar as propriedades entre 2 pontos diferentes.
Vamos lá resolver!
Passo 2
- A pressão manométrica na região 1.
- A altura H.
- A densidade de energia cinética e a potência no jato.
Como temos informações sobre a região 2, vamos usar a equação de Bernoulli entre 1 e 2. Como os dois estão na mesma altura, podemos cortar essa parte da equação:
Como 2 está em contato com a atmosfera, então .
Lembrando que , então a pressão manométrica em 1 vai ser:
Basta a gente calcular as velocidades em 1 e em 2. Mas como?
Passo 3
Usando a outra fórmula (lembra que só existem duas mesmo), o princípio da continuidade:
Para o ponto 2, como sabemos a vazão (), podemos usar que:
A seção reta do cano, em 2, é um círculo de diâmetro , então
Como
Agora para calcular podemos aplicar o princípio da continuidade (de novo) só que agora entre 1 e 2:
Passo 4
Podemos agora jogar na equação de Bernoulli:
Passo 5
Para poder incluir o H na equação, podemos usar a equação de bernoulli entre um ponto da superfície (vou chamar de ponto zero) e o ponto 2 (que já sabemos um monte de informações mesmo).
Os dois pontos escolhidos estão em contato direto com a atmosfera, então .
Se considerarmos o zero de altura como sendo altura do ponto 2, teremos e .
A velocidade no ponto 2 já calculamos antes ().
Já na superfície, como a área da superfície é muito maior do que a área do ponto 2, podemos considerar que a velocidade do líquido vai ser praticamente zero, pois o líquido vai descer muito lentamente.
Se você preferir ver isso matematicamente, pelo princípio da continuidade:
Como , então .
Substituindo tudo isso lá na equação de Bernoulli:
Passo 6
A energia cinética você lembra, né?
A densidade de energia cinética vai ser isso dividido pelo volume
Lembrando que
Teremos no ponto 2 (no jato):
Passo 3
Já a potência (energia por unidade de tempo), vai ser
Onde .
Como a energia potencial (U) vai ser constante, pois a região 2 está em altura constante,
Sabemos que , para obtermos K, basta multiplicar pelo volume,
Aqui, temos que lembrar que a variação de volume em relação ao tempo é justamente o que chamamos de vazão volumétrica (R):
Então,
Resposta
- ,