Há um recipiente cuja altura e área são dadas por e , respectivamente. Ele é conectado com um tubo cuja área é como mostrado na figura abaixo. O recipiente é cheio com um fluido de densidade de massa . A área do recipiente é suficientemente grande para podermos ignorar a velocidade da superfície do fluido (ponto A). Por outro lado, a pressão na saída do tubo (ponto B) é dada pela pressão atmosférica . Podemos ignorar o raio do tubo comparado com e . Considere a constante gravitacional conhecida.
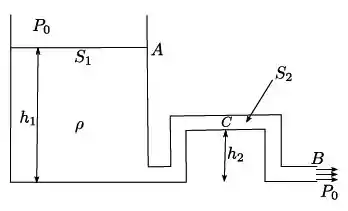
- Considerando que a saída do tubo fica na mesma altura que o fundo do recipiente, calcule a velocidade do fluido no ponto B.
- Calcule a pressão no ponto C, que fica a uma altura do fundo do recipiente.
Passo 1
a):
Bom, aqui é só a gente aplicar Bernoulli entro ponto e AAAH, mas e aquela voltinha ali no meio?
Não importa, importa apenas pro item b).
Nós sempre usamos Bernoulli entre dois pontos.
Atribuindo altura igual a zero no nível de , lembrando que as pressões em e são iguais pois os pontos estão em contato com a atmosfera e considerando a velocidade de igual a zero, temos que:
Passo 2
b):
Como a seção transversal de é igual a de , pela equação da continuidade:
Passo 3
Show? Agora vamos aplicar Bernoulli entre e
Resposta
a):
b):