Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Equação de Bernoulli

Ver Teoria
Exercício 68123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676970717273747576777879808182838485868788899091929394

Enunciado

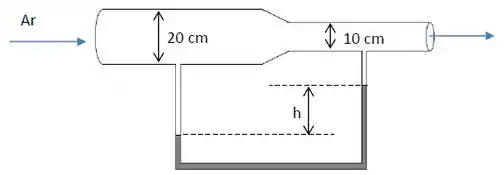
O ar escoa através de um tubo de vazão de 200 L / s . O tubo consiste em duas seções com diâmetros de 20 c m e 10 c m com uma seção de redução suave que as conecta. A diferença de pressão entre as duas seções do tubo é medida por u manômetro de água. Desprezando os efeitos de atrito e considerando a densidade do ar 1,20   k g / m 3 , determine:

(a) a velocidade do ar ao passar pelo tubo de maior diâmetro

(b) a razão entre as velocidades do tubo maior e o tubo menor

(c) a altura h entre as duas superfícies da água nas seções do tubo.

Passo 1

A vazão se relaciona com a velocidade do fluido por

R = A 1 v 1

No tubo de maior diâmetro A = π R 2 = π D / 2 2

R = 200 L s = 0,2   m 3 s

R = π D 2 2 v 1 → v 1 = 4 R π D 2 = 4 × 0,2 π × 0,2 2

v 1 = 6,37   m / s

Passo 2

A vazão é a mesma tanto no tubo maior quanto no tubo menor, ou seja

R = A 1 v 1 = A 2 v 2

Vamos chamar de 1 o tubo maior e de 2 o tubo menor. Assim a razão entre as velocidades é dada por

v 1 v 2 = A 2 A 1 = π D 2 2 2 π D 1 2 2 = D 2 D 1 2 = 0,1 0,2 2

v 1 v 2 = 1 4

Passo 3

A diferença de pressão entre os dois tubos é o que faz com que haja uma coluna de água a uma altura h em relação à interface água/ar. Assim podemos escrever

p 1 - p 2 = ρ á g u a g h

Passo 4

Pra achar essa diferença de pressão nos dois tubos podemos usar a equação de Bernoulli em dois pontos a mesma altura nos dois tubos

p 1 + 1 2 ρ a r v 1 2 + ρ a r g x = p 2 + 1 2 ρ a r v 2 2 + ρ a r g x

p 1 + 1 2 ρ a r v 1 2 = p 2 + 1 2 ρ a r v 2 2

Assim

p 1 - p 2 = 1 2 ρ a r v 2 2 - v 1 2

Na letra b vimos que

v 1 v 2 = 1 4 → v 2 = 4 v 1

Então a diferença de pressão fica

p 1 - p 2 = 1 2 ρ a r 4 v 1 2 - v 1 2 = 15 2 ρ a r v 1 2

Passo 5

Agora basta juntar os resultados dos passos 3 e 4

ρ á g u a g h = 15 2 ρ a r v 1 2

h = 15 2 ρ a r v 1 2 ρ á g u a g = 15 2 1,2 × 6,37 2 10 3 × 10

h = 0,0365   m

Resposta

(a)

v 1 = 6,37   m / s

(b)

v 1 v 2 = 1 4

(c)

h = 0,0365   m

Exercícios de Livros Relacionados

O tubo de Pitot (veja a figura) é usado para medir a velocidade do ar nos aviões. Ele é formado por um tubo externo com pequenos furos B (quatro são mostrados na figura) que permitem a entrada de ar n
Na figura, a água entra em regime laminar no lado esquerdo de uma tubulação (raio r 1 = 2,00R ), atravessa a parte seção central (raio R ), e sai pelo lado direito (raio r 3 = 3,00R ). A velocidade da
As linhas de correntes horizontais em torno das asas de um pequeno avião são tais que a velocidade sobre a superfície superior é igual a 70,0m/s e sobre a superfície inferior é igual a 60,0m/s. Se a á
A figura mostra um jorro d’água saindo por um furo a uma distância h = 10c m da superfície de tanque que contém H = 40c m de água. (a) A que distância x a água atinge o solo? (b) A que profundidade de
A água se move com uma velocidade de 5,0m / s em um cano com uma área de seção reta de 4,0c m 2 . A água desce gradualmente 10 m enquanto a seção reta aumenta para 8,0c m 2 . (a) Qual é a velocidade d