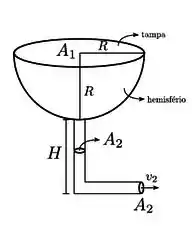
Uma caixa d'água hemisférica com raio R = 2 m está completamente cheia de água e com seu ponto mais baixo suspenso a uma altura H = 23 m do solo. O topo da caixa d'água está fechado com um teto plano na horizontal (ver figura). O fundo da caixa está conectado a um cano com 10 cm de raio e que se estende até o solo. Se a água no cano escoa em regime estacionário e com velocidade v2 = 20 m/s, determine:
(a) (1,0) A velocidade de escoamento da água no topo da caixa d’água.
(b) (2,0) Determine a pressão no topo da caixa d'água, entre a tampa e a superfície da água. Neste item considere que a velocidade no topo da caixa d'água é muito menor que a velocidade no cano v2.
Dados: Pressão atmosférica patm = Pa, densidade da água ρ = 103 kg/m3 e a aceleração gravitacional g = 10 m/s2.
Passo 1
a) Aqui a gente vai ter que usar o princípio da continuidade:
Substituindo:
Passo 2
b) Vamos aplicar Bernoulli entre os dois pontos:
Eu vou usar o ponto 2 como referencial, ok? Ou seja, no ponto 2: h2=0.
Queremos achar p1! O que nessa equação nós não temos? (Além de p1, claro.)
A pressão no ponto 2 vai ser a pressão atmosférica! Porque o ponto 2 está na atmosfera. Então:
Então nós temos tudo que precisamos! Vamos substituir:
A questão mandou considerar muito pequeno, então vamos anular a parcela que tem .
Resposta
a)
b)