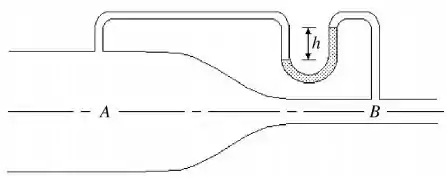
Água flui no tubo horizontal mostrado na figura abaixo. No ponto A, a área é de e a velocidade da água é de . Em B, a área é de . O fluido no tubo superior é mercúrio, que tem uma densidade de . Podemos tratar a água como um fluido ideal com uma densidade de .
Qual é a altura ?
ATENÇÃO: ESBOCE NA FIGURA ABAIXO AS LINHAS DE FLUXO E SE UTILIZAR BERNOULLI
INDIQUE OS PONTOS EM QUE A EQUAÇÃO FOI APLICADA.
A) B) C) D) E)
Passo 1
Bom, pela imagem, no lado esquerdo do mercúrio, temos uma pressão que equivale à , pressão que o “lado” do exerce sobre o mercúrio.
Por outro lado, no lado direito do mercúrio, temos uma pressão que equivale à , pressão que o “lado” do exerce sobre o mercúrio.
E a diferença de pressão entre esses dois lados é justamente a pressão da coluna de mercúrio de altura .
Sabendo disso, a gente precisa encontrar essa diferença de pressão !!
Passo 2
Pelo princípio da continuidade, temos que:
Substituindo os valores do enunciado:
E, então:
Passo 3
Ok!! Agora temos a velocidade no ponto ! Assim, podemos aplicar Bernoulli para achar a diferença de pressões em e , levando em consideração que os dois pontos estão na mesma altura ():
Passo 4
Agora sim! Como vimos no primeiro passo, a diferença de pressão entre e é justamente a pressão da coluna de mercúrio de altura :
Opa! Encontramos justamente o que queríamos!! E nossa resposta será a letra (d).
Resposta
Alternativa (d).