Considere um tanque onde a água pode escoar para fora passando por dois canos com seção retas de áreas diferentes. No exterior do tanque temos a pressão atmosférica . A área do cano exterior é e a do cano interior é . A altura é desconhecida, e a área do tanque é muito maior que a área dos canos. A vazão através do cano é de .
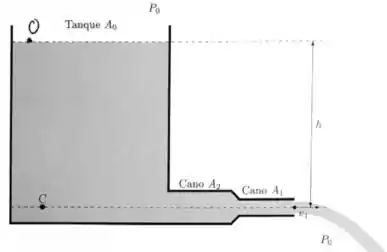
(a) Calcule a velocidade de saída da água.
(b) a velocidade da água ao longo do cano de área .
(c) a altura .
(d) a pressão manométrica dentro do cano de área .
(e) a pressão manométrica no ponto supondo que ele se encontra tão distante dos canos que a velocidade do fluido pode ser considerada nula.
Passo 1
Primeiro precisamos lembrar, ou saber haha, que a vazão de um liquído está relacionada com a área de escape de um fuido e pela velocidade que ele assume naquela região, ou seja
Perceba que mesmo que a estejamos olhando para lugares distinto de nosso cano, a vazão está relacionada com a quantidade de água que deixa todo o conjunto por segundo.
Outra relação que é muito importante baixar é a equação de bernoulli que nos da que
Passo 2
(a) Seguindo a relação do passo 1, podemos escrever a velocidade como
Na qual temos que , visto que cada , sendo assim temos
Assim dizemos que a velocidade da água que escoa pelo cano de área é dada por .
Passo 3
(b) Agora queremos saber a velocidade no cano que tem área transversal . Seguindo a mesma relação do passo anterior, temos que
assim
Ou seja, a velocidade é de . Ou seja, visto que a área é maior a relação mostra que a velocidade é menor.
Passo 4
(c) vamos usar a equação de bernoulli dada no passo 1 por
Vamos tomar , ou seja, o ponto mais alto do nosso tanque e o ponto mais próximo da saída do cano.
Assim nossa relação se desenvolve em
A ideia é que, na saída do cano, a pressão , assim temos que
Passo 5
(d) Agora vamos usar a mesma relação do item anterior, entretanto pegando pontos diferentes do anterior.
Queremos saber qual é a pressão dentro do cano de área . Logo parece muito provável que um dos pontos que precisamos é em , certo? E claramente o outro ponto que devemos tomar é a pressão no ponto . Já que sabemos o valor dela lá.
Assim temos que
Multiplicando tudo por e passando para o lado esquerdo, temos
Na qual é a pressão manométrica dentro do cano . Ou seja
E agora é conta hahaha
Passo 6
(e) Novameeeente vamos usar pela terceira vez a relação de Bernoulli, utilizada nos itens anteriores.
Só que agora temos a relação entre e .
Como estamos muito longe do cano, como sugere o problema, então temos que nossa velocidade é dita praticamente nula. Assim temos que nossa equação se transforma em
O que nos da que
E perceba que nosso , então
Ou seja, devido a vazão, a pressão no ponto é maior do que dentro do cano.