A figura mostra um sifão, que é um tubo usado para transferir líquidos de um recipiente para outro. O tubo ABC deve estar inicialmente cheio e nesta condição o líquido escoa pelo tubo até que a superfície do líquido no recipiente esteja no mesmo nível que a extremidade A do tubo. O líquido tem uma massa específica de 1000 kg/m³ e viscosidade desprezível. As distâncias mostradas na figura são h1= 25 cm e h2= 45 cm. Considere a área da seção reta do sifão constante.
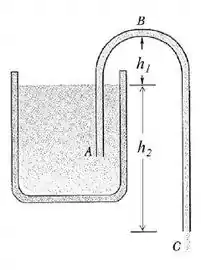
(a) Com que velocidade o líquido sai do tubo no ponto C?
b) Se a pressão atmosférica é , qual é a pressão do líquido em B, o ponto mais alto do tubo?
Passo 1
a) Para achar a velocidade em C, vamos aplicar Bernoulli. Mas eu vou aplicar Bernoulli entre o ponto C e um ponto D na altura da superfície do fluido, dentro do tubo. Assim ó:
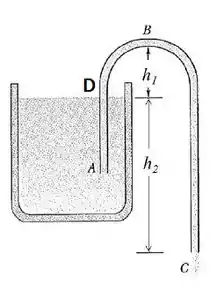
Então aplicando Bernoulli:
Eu vou tomar o ponto C como referencial, ok? Então .
As pressões e vão ser iguais à pressão atmosférica. Porque o ponto C está voltado para a atmosfera e o ponto D está na superfície do fluido onde a pressão é a atmosférica.
Ah, mas o fato de o ponto D estar dentro do tubo não influencia? NÃO, porque podemos aproximar a velocidade em D por zero. Então é como se fosse regime hidrostático.
A velocidade no ponto D também vai ser zero!
Eiiiii! Repara que se eu usasse o ponto A em vez do ponto D eu não poderia fazer essas aproximações! Então cuidado, não caia nessas pegadinhas.
Resumindo o rock, uma galera vai ser zerada ou cortada na equação de Bernoulli. Reescrevendo:
Passo 2
b) Vou aplicar Bernoulli de novo! Dessa vez entre os pontos B e D.
Veja que !
Por quê??????
Porque pequeno Padawan a área no tubo é constante! Pela equação da continuidade:
Substituindo então:
Passo 3
c) Ó, vou aplicar Bernoulli de novo entre os pontos B e D. Mas nesse caso h1 vai ser uma altura desconhecida que eu quero achar. Então:
Agora que vem o pulo do gato! Na altura máxima, a pressão vai ser zero! Então:
Resposta
a)
b)