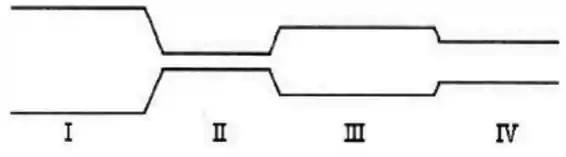
Um fluido passa por um tubo cuja seção reta varia conforme a figura abaixo. Em qual das seções ilustradas a pressão do fluido é mínima?

A pressão é sempre a mesma ao longo do tubo.

Para resolver essa questão precisamos relacionar a área do tubo com a pressão do fluido. De primeira vista não vemos nenhuma relação, certo?

Mas podemos relacionar a área com a velocidade do fluido, pelo principio da continuidade. Onde vimos que a vazão de um fluido não muda. Então:

Para manter a igualdade, se a área aumenta a velocidade deve diminuir e se a velocidade aumenta a área diminui.

Já relacionamos a área com a velocidade, mas e para relacionar a velocidade com pressão?

Para isso vamos usar a equação de Bernoulli e o fato de todos os estarem na mesma altura .

A equação de Bernoulli é escrita como:

Como todos os pontos estão na mesma altura , então a equação fica assim:

Então se a velocidade aumentar a pressão deve diminuir para a equação continuar sendo válida, e se a velocidade diminuir a pressão deve aumentar.

Beleza, encontramos todas as relações que precisamos.

Se a área aumenta a velocidade diminui, se a velocidade diminui a pressão aumenta. Então área maior igual à pressão maior.

Se a área diminui a velocidade aumenta, se a velocidade aumenta a pressão diminui. Então área menor igual à pressão menor.

Assim, teremos a menor pressão onde tivermos a menor área e temos a menor área no trecho .