Um reservatório A com superfície fechada, é conectado a um tubo B, aberto para a atmosfera, com área de seção reta constante e muito menor que a superfície de água em A, como mostra a figura.
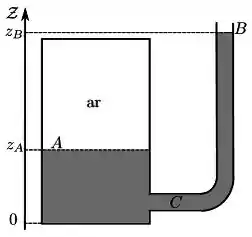
Considerando que existe um fluxo de água entre esses dois reservatórios, a velocidade da água no ponto C, indicado na figura, é dada por:
Passo 1
Temos aqui uma questão de hidrodinâmica. Vamos primeiro aplicar o princípio da continuidade entre B e C, que tem a mesma área de seção reta, então:
Se fizermos o mesmo entre B e A,
Mas como o enunciado diz que a área da seção reta de B é muito menor do que a de A, então podemos dizer que
Então, .
Usando essas informações, podemos aplicar a equação de Bernoulli entre A e B, já que a velocidade em B é a mesma que em C:
Passo 2
Usando a equação de Bernoulli entre A e B,
Como ,
Resposta
(c)