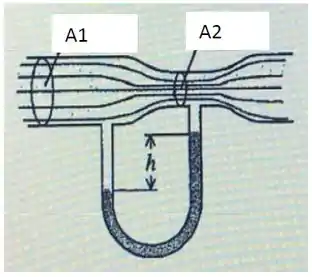
Em uma indústria química, álcool (Etanol) com densidade , escoa em regime laminar por um tubo cuja geometria é mostrada na figura. O líquido manométrico é o mercúrio e a diferença de altura determina a diferença de pressão entre os dois setores do escoamento.

a) Determine a diferença de pressão em atmosferas.

b) Determine a vazão do etanol sabendo que

Letra (b):

Vamos primeiro lembrar que a vazão é a mesma nos dois pontos (a massa de etanol é a mesma que passa pelas duas áreas):

E em relação aos raios, temos:

E vou elevar essa velocidade ao quadrado (você vai entender depois):

Aqui vamos guardar essa relação com muito carinho.

Agora vamos olhar pra equação da continuidade com os dois pontos em cima das áreas e na mesma altura:

Como temos a mesma altura , e temos o valor de que calculamos no item anterior, então vou reorganizar essa equação:

Lembra daquela relação que guardamos com carinho? Então, vou substituir aqui:

E colocando em evidência temos os parênteses que o problema nos disse que vale :

E vamos resgatar lá do passo anterior que a vazão em função do raio é , daí apareceu a vazão ao quadrado na nossa expressão!

Beleza?

Pronto pra próxima questão? =)