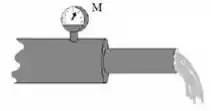
De modo a medir a vazão de saída de uma tubulação de água, foi instalado um manômetro (medidor de pressão que mede a diferença entre a pressão real e a pressão atmosférica). Ao final da tubulação, colocou-se uma restrição, cuja área de seção reta é igual a da área de seção reta da tubulação principal. O manômetro, colocado na posição mostrada na figura, indica pressão igual a . Determine o valor da velocidade de escoamento na saída da tubulação:
A) Faltam dados para determinar
B)
C)
D)
E)
Passo 1
Na situação do problema proposto valem a equação da continuidade e a equação de Bernoulli
Sendo () a velocidade (pressão) no tubo de maior diâmetro e () a velocidade (pressão) no tubo de menor diâmetro, temos que, sendo A a área de seção reta do tubo mais fino:
Considera-se primeiro a saída do tubo:
Pela equação da continuidade, a velocidade de escoamento no trecho mais fino e imediatamente após a saída do tubo são iguais. E já que estes dois pontos estão à mesma altura, pode-se escrever a equação de Bernoulli da forma:
Como , .
Passo 2
Agora, considerando o tubo mais grosso e o mais fino (1 e 2) teremos:
Como e fazendo umas continhas:
Passo 3
Agora, vamos usar Bernoulli nos pontos 1 e 2 (onde ):
Na prova foi dado que e no enunciado, (que é a pressão medida pelo manômetro no tubo mais grosso).
Isolando , que é igual ao :
Show!! Achamos o que o problema nos pediu. E nossa resposta será a letra (d)
Resposta
Alternativa (d).