Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Equação de Bernoulli

Ver Teoria
Exercício 11123456789101213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394

Enunciado

Equação da continuidade

Um fluido incompressível escoa suavemente pela tubulação mostrada na figura.

Assinale as relações corretas para as pressões e as velocidades do fluido nos pontos 1 , 2 , 3 e 4 indicados na figura:

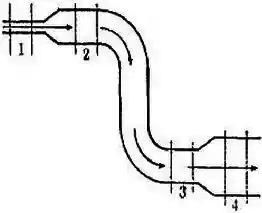
  1. p 1 > p 2 > p 3 > p 4 e v 1 > v 2 > v 3 > v 4
  2. p 1 = p 2 < p 3 = p 4 e v 1 > v 2 = v 3 > v 4
  3. p 1 > p 2 > p 3 > p 4 e v 1 < v 2 < v 3 < v 4
  4. p 1 < p 2 < p 3 < p 4 e v 1 > v 2 = v 3 > v 4

Passo 1

Para saber as relações entre pressões e velocidades, temos que aplicar a equação da continuidade (para velocidades) e a equação de Bernoulli (para pressões).

Vamos aplicar essas equações em cada par de pontos.

Passo 2

Equação da continuidade entre 1 e 2 :

A 1 v 1 = A 2 v 2

⇒ v 2 = A 1 A 2 v 1

Como A 1 < A 2 , então A 1 / A 2 < 1 .

Logo:

v 2 < v 1

Pelas alternativas, podemos eliminar a letra (c)!

Passo 3

Equação de Bernoulli entre 1 e 2 :

p 1 + 1 2 ρ v 1 2 + ρ g h 1 = p 2 + 1 2 ρ v 2 2 + ρ g h 2

Os pontos 1 e 2 estão à mesma altura.

Então:

h 1 = h 2

Eliminando os termos “ ρ g h ” nas equação de Bernoulli, temos:

p 1 + 1 2 ρ v 1 2 = p 2 + 1 2 ρ v 2 2

⇒ p 1 + 1 2 ρ v 1 2 - 1 2 ρ v 2 2 = p 2

⇒ p 2 = p 1 + 1 2 ρ v 1 2 - v 2 2

Como v 1 > v 2 , então v 1 2 - v 2 2 > 0

Logo: p 2 > p 1

Pelas alternativas, podemos eliminar as letras (a) e (b).

Então fechou! Só restou a alternativa (d)!

Nem precisamos continuar a questão!

Passo 4

Mas se você quiser conferir, vamos fazer o resto, de um modo mais rápido:

Equação da continuidade entre 2 e 3 :

A 2 v 2 = A 3 v 3

Como as áreas são iguais:

v 2 = v 3

Passo 5

Equação de Bernoulli entre 2 e 3 :

p 2 + 1 2 ρ v 2 2 + ρ g h 2 = p 3 + 1 2 ρ v 3 2 + ρ g h 3

Como as velocidades são iguais:

p 2 + ρ g h 2 = p 3 + ρ g h 3

⇒ p 3 = p 2 + ρ g h 2 - h 3

Como h 2 > h 3 :

p 3 > p 2

Passo 6

Equação da continuidade entre 3 e 4 :

A 3 v 3 = A 4 v 4

Como A 3 < A 4 :

v 3 > v 4

Passo 7

Equação de Bernoulli entre 3 e 4 :

p 3 + 1 2 ρ v 3 2 + ρ g h 3 = p 4 + 1 2 ρ v 4 2 + ρ g h 4

Como h 3 = h 4 :

p 3 + 1 2 ρ v 3 2 = p 4 + 1 2 ρ v 4 2

⇒ p 4 = p 3 + 1 2 ρ v 3 2 - v 4 2

Como v 3 > v 4 :

p 4 > p 3

Passo 8

Ordenando as pressões e velocidades, encontramos exatamente como está na alternativa (d):

p 1 < p 2 < p 3 < p 4

v 1 > v 2 = v 3 > v 4

Resposta

Alternativa (d).

Exercícios de Livros Relacionados

O tubo de Pitot (veja a figura) é usado para medir a velocidade do ar nos aviões. Ele é formado por um tubo externo com pequenos furos B (quatro são mostrados na figura) que permitem a entrada de ar n
Na figura, a água entra em regime laminar no lado esquerdo de uma tubulação (raio r 1 = 2,00R ), atravessa a parte seção central (raio R ), e sai pelo lado direito (raio r 3 = 3,00R ). A velocidade da
As linhas de correntes horizontais em torno das asas de um pequeno avião são tais que a velocidade sobre a superfície superior é igual a 70,0m/s e sobre a superfície inferior é igual a 60,0m/s. Se a á
A figura mostra um jorro d’água saindo por um furo a uma distância h = 10c m da superfície de tanque que contém H = 40c m de água. (a) A que distância x a água atinge o solo? (b) A que profundidade de
A água se move com uma velocidade de 5,0m / s em um cano com uma área de seção reta de 4,0c m 2 . A água desce gradualmente 10 m enquanto a seção reta aumenta para 8,0c m 2 . (a) Qual é a velocidade d