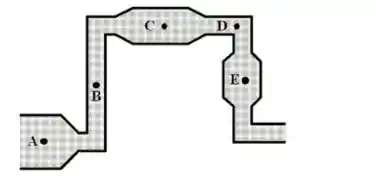
Um sistema horizontal de tubos, que proporciona um fluxo constante de água, é construído a partir de tubos com diferentes diâmetros, como mostrado na figura abaixo. Em qual dos pontos marcados a água no tubo apresenta maior pressão? O desenho é uma vista de cima do tubo.

1. A
2. B
3. C
4. D
5. E

Bora analisar toda a tubulação agora. Perceba, antes disso, que todos os pontos estão na mesma altura, já que estamos vendo a tubulação de cima e não de lado.

Vamos supor que a água entra na tubulação, no ponto , com velocidade e pressão . Após isso, o fluxo de água segue para , passando a ter uma pressão Assim, podemos relacionar os dois pontos por Bernoulli:

Onde é dado pela equação da continuidade:

Assim:

Vamos agora analisar o ponto e o , seguindo o mesmo princípio:

Analisando a velocidade em

Assim:

E agora, o ponto e

Analisando a velocidade em

Assim:

E por fim, o ponto e

Analisando a velocidade em

Assim:

Então, no final das contas, descobrimos que a pressão em é maior que todas as pressões.:

Assim: