Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Equação de Bernoulli

Ver Teoria
Exercício 41235678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394

Enunciado

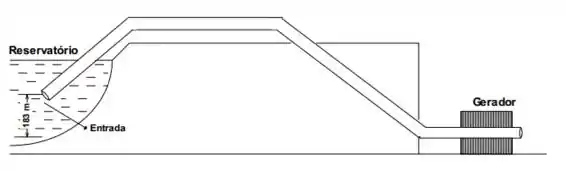
A área de entrada do tubo inferior do reservatório indicado na figura a seguir vale 0,75   m 2 . A água entra neste tubo com uma velocidade de 0,40   m/s . No gerador, instalado a uma profundidade de 183   m abaixo do nível de entrada deste tubo, a área da seção reta é igual a 0,032   m 2 e a água escoa com uma velocidade de 9,4   m/s nesta saída. Calcule a diferença de pressão em N / m 2 entre a entrada e a saída. ρ H 2 O = 10 3   kg / m 3

g = 10   m / s 2

Passo 1

Nessa questão, utilizaremos a equação de Bernoulli:

p 1 + 1 2 ρ 1 v 1 2 + ρ 1 g h 1 = p 2 + 1 2 ρ 2 v 2 2 + ρ 2 g h 2

Primeiramente, vamos identificar as informações disponíveis e o que devemos descobrir:

O que sabemos:

v 1 = 0,40   m / s v 2 = 9,4   m / s h 1 = 183   m     h 2 = 0 ρ 1 = ρ 2 = ρ H 2 O = 10 3   kg / m 3

O que queremos saber:

∆ p = p 2 - p 1  

Note:

Consideramos o escoamento incompressível ( ρ 1 = ρ 2 ) , já que nada foi dito que contraria isso. Além disso, notou que não precisamos saber os valores das pressões e sim apenas a variação? Partiu calcular ∆ p ?(:

Passo 2

Bom, vamos agora aplicar os valores na equação:

p 1 + 1 2 ρ 1 v 1 2 + ρ 1 g h 1 = p 2 + 1 2 ρ 2 v 2 2 + ρ 2 g h 2

p 1 + 1 2 ⋅   10 3 ⋅   0,40 2 + 10 3 ⋅ 10 ⋅ 183 = p 2 + 1 2 ⋅ 10 3 ⋅ 9,4 2 + 10 3 ⋅ 10 ⋅ 0

1 2 ⋅   10 3 ⋅   0,40 2 + 10 3 ⋅ 10 ⋅ 183 - 1 2 ⋅ 10 3 ⋅ 9,4 2 = p 2 - p 1 = ∆ p  

Fazendo os cálculos, obtemos ∆ p = 1785900

Arredondando para um algarismo significativo após a vírgula:

∆ p = 1,8 ⋅ 10 6   Pa = 1,8.10 6 N / m 2

Lembrando que:

1 P a = 1 N / m 2

(:

Resposta

∆ p = 1,8 ⋅ 10 6 N / m 2

Exercícios de Livros Relacionados

O tubo de Pitot (veja a figura) é usado para medir a velocidade do ar nos aviões. Ele é formado por um tubo externo com pequenos furos B (quatro são mostrados na figura) que permitem a entrada de ar n
Na figura, a água entra em regime laminar no lado esquerdo de uma tubulação (raio r 1 = 2,00R ), atravessa a parte seção central (raio R ), e sai pelo lado direito (raio r 3 = 3,00R ). A velocidade da
As linhas de correntes horizontais em torno das asas de um pequeno avião são tais que a velocidade sobre a superfície superior é igual a 70,0m/s e sobre a superfície inferior é igual a 60,0m/s. Se a á
A figura mostra um jorro d’água saindo por um furo a uma distância h = 10c m da superfície de tanque que contém H = 40c m de água. (a) A que distância x a água atinge o solo? (b) A que profundidade de
A água se move com uma velocidade de 5,0m / s em um cano com uma área de seção reta de 4,0c m 2 . A água desce gradualmente 10 m enquanto a seção reta aumenta para 8,0c m 2 . (a) Qual é a velocidade d