Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Equação de Bernoulli

Ver Teoria
Exercício 63123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616264656667686970717273747576777879808182838485868788899091929394

Enunciado

Física Termodinâmica e Ondas – Young e Freedman – 12 edição – Capítulo 14 – Exercício 44.

(Cap 14 - Ex 44) Uma bebida leve (essencialmente água) escoa em um tubo de uma fábrica de cerveja com uma vazão volumétrica tal que deve encher 220 latas de 0,355 L por minuto. Em um ponto do tubo, a pressão manométrica é igual a 152kPa, e a área da seção reta é igual a 8,0 c m 2 . Em um ponto 1, situado 1,35m acima do ponto 2, a área da seção reta é igual a 2,0 c m 2 . Obtenha a) a vazão mássica; b) a vazão volumétrica; c) as velocidades do escoamento nos pontos 1 e 2; d) a pressão manométrica no ponto 1.

Passo 1

E ai seres de luz, show de bola?

Bora lá?

Sabemos que por teoria a densidade é dada como

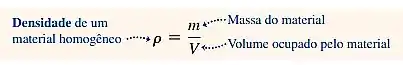
Aqui, aplicaremos a equação de continuidade e a equação de Bernoulli aos pontos 1 e 2.

A densidade da agua é de 1 k g / L

Passo 2

  1. Logo, temos que a vazão é de

    2. A taxa de fluxo de massa     d m / d t  

    220 ⋅ 0,355   k g 60   s = 1,30   k g / s

    Passo 3

  2. A densidade do liquido é

    3. ρ = d V d t  

    0,355   k g 0,355 × 10 - 3   m 3 = 1000   k g / m 3

    E assim, a taxa de fluxo de volume é

    1,30 k s s 1000 k g m 3

    = 1,30 × 10 - 3   m 3 / s

    = 1,30 L / s

    Outra forma de obter este resultado e da seguinte maneira:

    220 ⋅ 0,355   L 60   s = 1,30   L / s

    Passo 4

  3. E as velocidades de escoamento nos pontos 1 e 2 são dados, respectivamente, por

    4. Pela vazão volumétrica (h)

    d V d t = 1.30 × 10 - 3 m 3 / s

    Sabemso qu

    d V d t = A 1 v 1

    v 1 = d V d t ( A 1 )

    v 1 = 1,30 × 10 - 3   m 3 / s 2 × 10 - 4   m 2 = 6,50   m / s

    Pela equação de continuidade

    A 1 v 1 = A 2 v 2

    v 2 = A 1 A 2 v 1

    = 2 8 v 1

    = 1 4 v 1

    v 2 = 6.50 4

    v 2 = 1,6 3   m / s

    Passo 5

  4. E a pressão manométrica no ponto 1

p 1 = p 2 + 1 2 ρ v 2 2 - v 1 2 + ρ g y 2 - y 1

Esbocando para melhor visualização

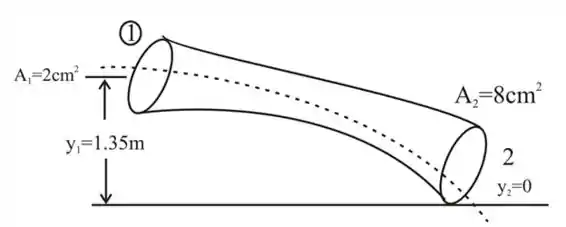
  p 1 = 152   k P a + 1 2 ( 1 00 k g / m 3 )   1,63   m / s 2 - 6,50   m / s 2 - ( 1000   K g / m 3 ) ( 9.80   m / s 2 ) ( 1.35   m )

= 119   k P a

O aumento da altura e o aumento da velocidade do fluido no ponto 1 causam a pressão no ponto 1 para ser menor que a pressão no ponto 2.

Resposta

  1. 1,30 k g s
  2. 1,30 L s
  3. 1,64   m / s
  4. 119   k P a

Exercícios de Livros Relacionados

O tubo de Pitot (veja a figura) é usado para medir a velocidade do ar nos aviões. Ele é formado por um tubo externo com pequenos furos B (quatro são mostrados na figura) que permitem a entrada de ar n
Na figura, a água entra em regime laminar no lado esquerdo de uma tubulação (raio r 1 = 2,00R ), atravessa a parte seção central (raio R ), e sai pelo lado direito (raio r 3 = 3,00R ). A velocidade da
As linhas de correntes horizontais em torno das asas de um pequeno avião são tais que a velocidade sobre a superfície superior é igual a 70,0m/s e sobre a superfície inferior é igual a 60,0m/s. Se a á
A figura mostra um jorro d’água saindo por um furo a uma distância h = 10c m da superfície de tanque que contém H = 40c m de água. (a) A que distância x a água atinge o solo? (b) A que profundidade de
A água se move com uma velocidade de 5,0m / s em um cano com uma área de seção reta de 4,0c m 2 . A água desce gradualmente 10 m enquanto a seção reta aumenta para 8,0c m 2 . (a) Qual é a velocidade d