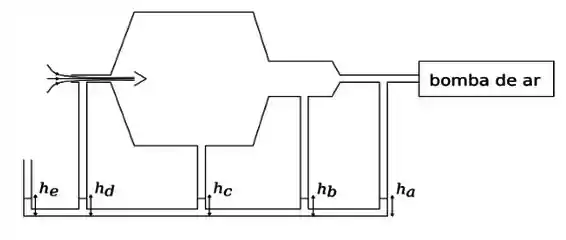
Qual a sequência correta entre as alturas ?
é a altura da coluna de líquido que repousa na parte de baixo do tubo.
Passo 1
Primeiro, vamos entender como a altura do liquido se relaciona com a pressão do ar lá no tubo.
Onde a pressão do ar for maior, a altura do líquido em baixo , será menor, pois no fundo a pressão deve ser igual para todos os pontos e para que ocorra essa igualdade entre a pressões, a altura do líquido vai compensar a pressão causada pelo ar.
Então onde a pressão do ar for pequena a altura do líquido será maior, e onde for grande a pressão do ar a altura do liquido será pequena,
Bem, e como comparar as pressões do gás?. A equação de Bernoulli, nos permite relacionar a velocidade de um fluido em um tubo com a pressão do fluido, certo?
Como todos os pontos estudados estão na mesma altura, temos então, que a diferença de pressão ocorrerá devido a diferença entre as velocidades do ar, no ponto certo?
Mas, não temos nenhum dado sobre as velocidade, certo? Errado, temos pela imagem a área da secção reta do tubo, e pelo principio da continuidade, sabemos que
Então quanto maior a área do tubo, menor a velocidade, para que se respeite a continuidade de massa do fluido.
Assim, temos que
Vamos deixar o ponto de lado, pois ele já sabemos que está na pressão atmosférica.
Devido a relação das áreas da secção reta dos tubo, podemos então relacionar as velocidade
Agora, voltamos a equação de Bernoulli, onde já vimos que quanto maior a velocidade menor será a pressão exercida pelo fluido, assim
Podemos entende a pressão atmosférica, quando a velocidade é do ar é zero, assim
Agora a última relação, que lá no início, vimos que quanto maior a pressão do ar, menor seria a altura do líquido.
Assim,
Resposta
Alternativa