Um riacho de efluentes industriais líquidos () de largura e profundidade corre a céu aberto.
O riacho passa a ser canalizado em uma tubulação com seção reta circular de diâmetro , que corre ao longo da horizontal de modo que o seu eixo central está a abaixo do nível médio do rio.
Finalmente, o líquido é lançado num jato horizontal para a atmosfera.
Observa-se que a velocidade do riacho, , é aproximadamente horizontal e uniforme ao longo de toda seção reta. Considere os fluxos sempre laminares e uniformes. Considere e .
Dado:
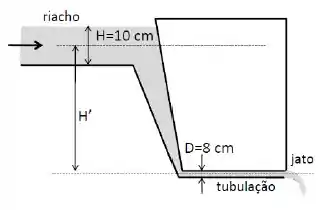
- Calcule a vazão do riacho.
- Calcule a velocidade do líquido dentro da tubulação horizontal.
- Calcule a pressão num ponto qualquer dentro da tubulação.
- Calcule a profundidade da tubulação.
Passo 1
a):
Pra descobrir a vazão podemos pensar na seção transversal do riacho e relacioná-la com a sua velocidade.
Sabendo que a área transversal será dada por:
A vazão será o produto dessa área pela velocidade:
Passo 2
b):
Vamos usar o princípio da continuidade aqui. Como a vazão é constante, a vazão na tubulação será a mesma que a do riacho. Bem, essa vazão, a da tubulação, será dada por:
Sendo que a área da tubulação pode ser calculada usando-se o raio da tubulação (metade do diâmetro). Logo:
Logo a área será:
Logo:
Passo 3
c):
Vamos usar Bernoulli pra comparar um ponto no jato com um ponto no interior do tubo. Os dois pontos terão a mesma altura e a mesma velocidade, então:
Onde as variáveis com índice 2 indicam o ponto do jato e as de índice 1 o ponto no interior do tubo.
Bom, e , logo:
No entanto, a pressão em 2 é a pressão atmosférica. Então:
Passo 4
d):
Vamos comparar aqui um ponto no meio do riacho com um ponto na tubulação. Vamos usar Bernoulli, e pra isso vamos considerar o nível de potencial gravitacional zero o nível da tubulação.
Além disso, lembrando que , consideremos que . Então a equação de Bernoulli fica:
Como , , , e :
Resposta
a):
b):
c):
d):