Um tubo cilíndrico fechado de raio R e comprimento H é preenchido por um fluido de densidade ρ e colocado na vertical, conforme a figura ao lado. Um pequeno furo de raio na extremidade inferior do tubo é tampado por uma rolha. A pressão atmosférica é e a aceleração da gravidade é .
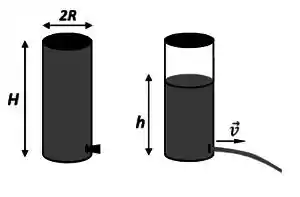
(a) Determine a força que o líquido exerce sobre a rolha.
(b) Determine a velocidade com a qual o fluido escoa pelo furo em função da altura h do líquido.
Determine a altura em que o fluido para de escoar.
Passo 1
A força que a rolha sofre é a força causada pela pressão de liquido. A pressão de liquido é
Assim a força causada por essa pressão é
Passo 2
Como o tubo é fechado a pressão dentro dele na superfície do liquido é zero.
Assim, aplicando a equação de Bernoulli, na superfície do liquido a uma altura e na saído do furo temos:
A pressão já falamos que é zero, a velocidade também podemos considerar zero. E o referencial que usamos a altura do furo é zero. Assim, a equação fica:
Passo 3
O fluido vai parar de sair quando a velocidade for zero, certo? E quando isso acontecerá?
Pela equação da velocidade vemos que ela será zero quando houver a seguinte igualdade:
Assim, a altura mínima é: