Um tanque aberto na parte superior contém uma grande quantidade de água (de densidade ) que pode ser esgotada por meio de um cano ligado à sua parte inferior. A secção reta do cano na região do ponto , localizado a uma altura abaixo do nível da água, é , e na região , localizado a uma altura abaixo de , é . No final do encanamento existe uma válvula . Considere que a área da superfície do tanque é muito maior que área da secção reta da tubulação. Calcule:
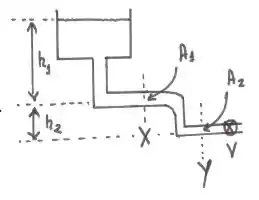
- A pressão nos pontos e com a válvula fechada.
- A velocidade da água no ponto com a válvula aberta.
- A pressão no ponto com a válvula aberta.
Passo 1
a):
Primeeeeiro de tudo, vamos definir dois pontos: ponto A na superfície do tanque, a uma altura igual a , e ponto B nas proximidades da válvula V com altura igual a zero. Repare que eu to tomando o ponto B como referência.
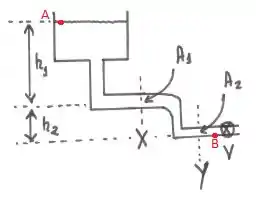
Show, agora podemos continuar.
Aqui nós podemos aplicar stevin, já que não há escoamento e, logo, estamos no regime hidrostático.
Então, a pressão no ponto X vai ser igual a pressão de mais a pressão causada pela coluna de fluido. Como está aberta pra atmosfera, vamos chamar a pressão de de . Logo:
Analogamente, a pressão em será:
Passo 2
b):
Beleza, agora vamos mudar nossa lógica e aplicar Bernoulli.
Agora o referencial de altura zero está em . Além disso, como está próximo da abertura do cano, a pressão em é Então, aplicando Bernoulli entre e
Passo 3
c):
Agora pra achar a pressão em , nós vamos aplicar Bernoulli entre e . Pra isso a gente precisa do valor da velocidade em . Vamos usar o principio da continuidade entre e pra achar isso:
Agora, aplicando Bernoulli:
Resposta
a):
b):
c):