Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Equação de Bernoulli

Ver Teoria
Exercício 24123456789101112131415161718192021222325262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091929394

Enunciado

UFRJ – Física 2 2020.2 – P1 – Questão 9

v a r é formado por um tubo em U aberto nas duas extremidades e preenchido por dois líquidos imiscíveis de densidades e Embora aberta, uma das extremidades é mantida protegida do vento, como mostra a figura.

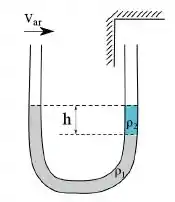
Determine v a r em função da aceleração da gravidade g , da densidade do ar no local ρ a r e dos parâmetros indicados na figura.

Escolha uma:

  1. v a r = ρ 1 ρ a r g h
  2. v a r = ρ 2 ρ a r g h
  3. v a r = 2 ρ 2 - ρ 1 ρ a r g h
  4. v a r = 2 ρ a r ρ 1 - ρ 2 g h
  5. v a r = ρ a r ρ 2 - ρ 1 g h
  6. v a r = 2 ρ 1 ρ 2 g h
  7. v a r = 2 ρ 1 - ρ 2 ρ a r g h
  8. v a r = 2 g h

Passo 1

Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?

Vou começar aplicando a equação de conservação nas duas extremidades do tubo. Na extremidade da direita, a que está protegida do vento, teremos apenas que levar em consideração os termos das pressões dos líquidos. Já na extremidade da esquerda teremos apenas o termo da velocidade do ar:

ρ a r v a r 2 2 = ρ 1 g h - ρ 2 g h

ρ a r v a r 2 2 = g h ( ρ 1 - ρ 2 )

v a r 2 2 = ρ 1 - ρ 2 ρ a r g h

v a r = 2 ρ 1 - ρ 2 ρ a r g h

Passo 2

Então analisando as alternativas vemos que a opção correta é a letra (g).

Beleza?

Pronto pra próxima questão? =)

Resposta

( g )

Exercícios de Livros Relacionados

O tubo de Pitot (veja a figura) é usado para medir a velocidade do ar nos aviões. Ele é formado por um tubo externo com pequenos furos B (quatro são mostrados na figura) que permitem a entrada de ar n
Na figura, a água entra em regime laminar no lado esquerdo de uma tubulação (raio r 1 = 2,00R ), atravessa a parte seção central (raio R ), e sai pelo lado direito (raio r 3 = 3,00R ). A velocidade da
As linhas de correntes horizontais em torno das asas de um pequeno avião são tais que a velocidade sobre a superfície superior é igual a 70,0m/s e sobre a superfície inferior é igual a 60,0m/s. Se a á
A figura mostra um jorro d’água saindo por um furo a uma distância h = 10c m da superfície de tanque que contém H = 40c m de água. (a) A que distância x a água atinge o solo? (b) A que profundidade de
A água se move com uma velocidade de 5,0m / s em um cano com uma área de seção reta de 4,0c m 2 . A água desce gradualmente 10 m enquanto a seção reta aumenta para 8,0c m 2 . (a) Qual é a velocidade d