A água sai de uma torneira aberta de forma a formar um feixe que se afina, sem se dividir, conforme a água flui em direção ao ralo, como indica a figura. Supondo que a seção transversal deste feixe se mantém circular no decorrer do fluxo, com raio e velocidade da água imediatamente após sair da torneira, e considerando a água um fluido incompressível sem viscosidade (considere a aceleração da gravidade conhecida), estime:
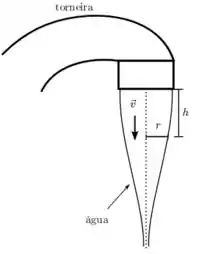
- A velocidade do fluido , em função da diferença de altura a partir da torneira.
- O raio de seção transversal do feixe, em função do módulo de velocidade nesta seção do fluido.
- O raio de uma seção transversal de um feixe, , agora em função da diferença de altura a partir da torneira.
Passo 1
a):Vamos usar Bernoulli aqui!
Vamos fazer assim: O ponto de altura zero será o ponto onde as moléculas do fluido terão uma velocidade . A altura cresce de baixo pra cima.
Então, calculando entre esse ponto e o ponto da boca da torneira:
Passo 2
b):
Aqui a gente usa o principio da continuidade, ou seja:
Vamos tomar como a vazão que a gente calcula bem na boca da torneira. Como ela tem raio
Então:
A outra vazão é calculada pelo produto da área da seção que vai diminuindo( pela velocidade . Então:
Igualando as duas:
Passo 3
c):
Po, bem tranquila essa. Já temos a equação da velocidade em função da altura em a), basta a gente substituir na equação encontrada em b):
Resposta
a):
b):
c):