James Stewart – Cálculo Volume 2 – Tradução da 7ª edição americana. Capítulo 14 Seção 3 Problema 11.
(Cap 14.3 – Ex 11) Se , encontre e interprete esses números como inclinações. Ilustre com esboços desenhados à mão ou gráficos de computador.
Passo 1
Falaiii, moçadinha, shwo de bola?
Bora resolver essa juntinho comigo?
Simboráaa
Sabemos que...
Para determinar derivadas parciais, é necessário fixar as variáveis que não estão envolvidas na derivação e tratá-las como valores constantes.
Passo 2
Seja . Para determinar fixamos o valor de y e derivamos em relação a . Assim, temos: . Para determinar , fixamos o valor de x e derivamos em relação a y. Assim, temos: .
Passo 3
Agora basta substituir os valores de x e y, respectivamente, nas derivadas parciais encontradas.
Passo 4
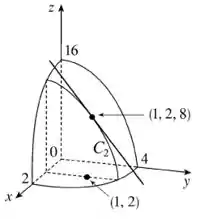
Interpretação da derivada parcial: em determinado ponto, ela representa a inclinação da reta tangente ao ponto da curva obtida quando “cortamos” a função com um plano de um valor x ou y constantes. Veja as imagens a seguir, as quais irão auxiliar no seu entendimento.
Quando a derivada parcial é em relação a x:
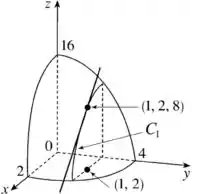
Quando a derivada parcial é em relação a y:
