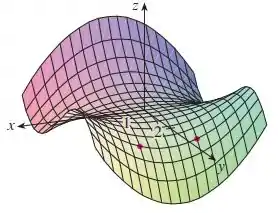
(Cap 14.3 – Ex 6) Determine os sinais das derivadas parciais da função f cujo gráfico é mostrado
Passo 1
Falaiii, moçadinha, shwow de bola?
Bora resolver essa juntinho comigo?
Simboráa
O que essa questão quer da gente é que a gente ache o sinal das derivadas parciais. Mas o problema é que o enunciado não dá a função pra gente derivar. Então como vamos fazer isso?
O que o enunciado dá pra gente é um gráfico. Então o que a gente vai precisar fazer é olhar pra esse gráfico e ver como a função se comporta. Quando a função decresce, a derivada é negativa. E quando a função cresce, ela é positiva. Entendeu?
Mas tem um detalhe a mais aqui! Pra calcular a derivada parcial com relação , vamos precisar fixar um valor de , que no caso é , pois queremos a derivada parcial no ponto .
E pra calcular a derivada com relação a , a gente vai fixar um valor pra , que vai ser .
Bora lá ver como vai ficar isso!
Passo 2
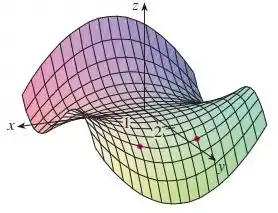
- Para determinar o sinal de , fixamos e verificamos a variação de . Então vamos olhar pro gráfico! , sSeguindo no sentido positivo do eixo e partindo de ,. Oobserva-se que a função decresce, isto é, é negativo.
- Para determinar o sinal de , fixamos e verificamos a variação de y, seguindo no sentido positivo do eixo y e partindo de y = 2. Observa-se que a função decresce, isto é, é negativo.
- Negativo
- Negativo
Passo 23
Resposta
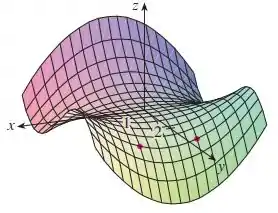
Resposta
Ei, a resposta está no passo a passo :)