Passo 1
Esse tipo de questão tem que ser resolvida de dentro para fora. Vamos iniciar fazendo uma amperiana no interior do cilindro menor, com um raio . Nesse caso, precisamos calcular a densidade de corrente do cilindro pequeno para começar.
Multiplicando essa densidade pela área envolvida, temos:
Por isso, nesse caso, pela lei de Ampère:
E aí a corrente cresce linearmente.
Passo 2
Para os casos em que a amperiana é um cilindro com raio: , temos que a corrente envolvida será sempre a mesma: a corrente do cilindro menos, que equivale a . Por isso, nessa situação:
Aqui a corrente decresce.
Passo 3
Quando chegamos a , toda a corrente do cilindro maior se concentra sobre uma superfície, temos uma densidade superficial e a corrente interna à amperiana cai repentinamente para zero.
Pois quando a corrente interna passa a ser . Elas se subtraem porque correm em sentidos opostos.
Então:
Passo 4
E no caso em que ? Bom, nessa situação o campo vai ser igual a metade do que calculamos no passo , fazendo . Isso acontece porque, nessa situação, temos que fazer uma “média”.
Passo 5
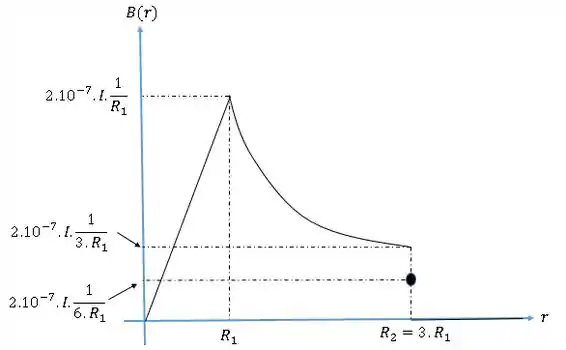
Desenhando o gráfico e fazendo :
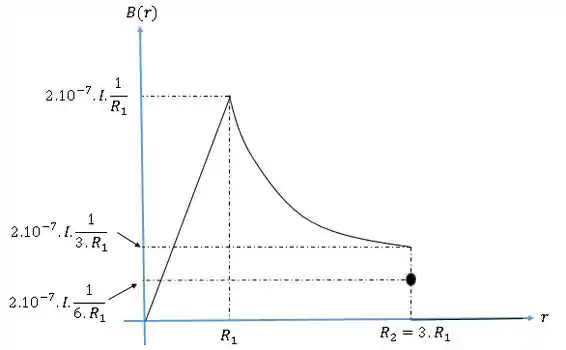
Resposta
(a)
(b)