Um cabo coaxial consiste em um cilindro condutor maciço, infinito, de raio coaxial a uma casca condutora cilíndrica, também infinita, de raio e espessura desprezível. Uma seção transversal deste cabo é mostrada na figura abaixo. O cilindro transporta uma corrente estacionária de intensidade , uniformemente distribuída sobre sua seção transversal e com sentido para fora do plano da folha, enquanto a casca transporta uma corrente estacionária de mesma intensidade no sentido inverso.
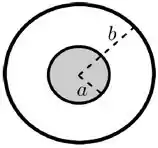
Determine o campo magnético produzido pelo cabo (módulo, direção e sentido) em um ponto a uma distância do eixo. Considere todas as regiões distintas do espaço, dadas por (i) , (ii) e (iii) . Justifique cuidadosamente todo o desenvolvimento.
Passo 1
Antes de qualquer coisa, vamos descobrir qual vai ser o formato da expressão do campo elétrico. Se colocarmos o cabo em um sistema de coordenadas tal que o eixo seja o eixo que passa pelo seu centro, o campo magnético será
Mass nesse problema temos simetria de translação ao longo do eixo , então as componentes do campo magnético não podem depender nem de nem de .
O campo também não pode ter componente radial, pois o fluxo de campo magnético na superfície gaussiana cilíndrica seria não nulo, o que violaria a Lei de Gauss para o magnetismo.
Além de tudo isso, o campo também não pode ter componente , pois todos os elementos de corrente infinitesimal desse sistema estão ao longo do eixo , logo, a Lei de Biot-Savart implica em um campo transversal a essa direção.
Finalmente, concluímos que o campo magnético tem o formato:
Onde é o vetor unitário da direção circunferencial e é dado pela regra da mão direita a partir de , no caso, é o sentido anti-horário da figura do enunciado.
Passo 2
Agora precisamos escolher uma curva amperiana circular de raio .
Essa curva vai estar no mesmo sentido do campo, coincidindo com uma linha de campo, logo, a circulação de campo nessa curva será
Sabendo que tem o mesmo valor em todos os pontos de (pois estão à mesma distância do eixo)
Como nossa curva amperiana é circular e tem raio
Agora só precisamos usar a Lei de Ampére em cada uma das regiões ;)
Passo 3
Para utilizar a Lei de Ampére, vamos lembrar que o sentido positivo da corrente vai ser o plano pra fora do papel () já que foi a orientação de que encontramos no passo 1.
Para cada uma das regiões:
i)
Nesse caso, a curva escolhida não está englobando totalmente a corrente do cilindro.
Sabemos que a corrente é uniformemente distribuída, então, o módulo da densidade de corrente é dado por
Logo, a corrente total que atravessa uma superfície delimitada por é
Agora que sabemos a corrente na superfície, podemos aplicar na Lei de Ampére:
Passo 4
ii)
Agora, a curva amperiana engloba totalmente toda a corrente no cilindro, então
Então, na Lei de Ampére
Note que a expressão é a mesma da de um campo magnético produzido por um fio fino, retilíneo e infinito, o que já era esperado pela simetria do problema :)
Passo 5
iii)
Agora, a amperiana ainda engloba toda a corrente no cilindro, mas engloba a da casca também. Como essas duas correntes têm módulo igual e sentidos opostos, temos que
Logo