Em um modelo clássico para o átomo de hidrogênio, um elétron se desloca em movimento circular uniforme com velocidade escalar e raio em torno de um próton fixado na origem. Supondo que a corrente associada ao movimento do elétron pode ser tratada como uma corrente estacionária, qual é a intensidade do campo magnético produzido por ela na posição do próton?
Passo 1
Como o problema pede para que associemos ao movimento circular do elétron uma corrente estacionária, então essa corrente produzirá um campo igual ao campo produzido por uma corrente numa espira circular. Então, o elétron seguiria a trajetória desenhada abaixo.

Nesse caso, então, o campo no centro onde está o próton pode ser escrito usando lei de Ampère. A nossa amperiana será essa circunferência desenhada em vermelho centrada no elétron
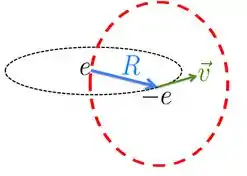
Assim, pela lei de Ampère
O que precisamos fazer agora é ver qual como escrever a corrente para esse elétron!! Vamo lá...segue aí..
Passo 2
A corrente nada mais é do que quantidade de carga por unidade de tempo, correto? Bom, mas nesse caso, a carga é a carga do elétron e temos que considerar a corrente associada a essa carga após ela percorrer o comprimento do círculo. Então, a gente pode escrever o seguinte
sendo que é o período que o elétron gasta para percorrer o comprimento da espira.
Então, olha só, como o movimento é circular, a velocidade da carga é a razão entre o deslocamento dela dividido pelo tempo que ela gasta para percorrer a espira toda uma vez. Isto é,
Como isso, a corrente associada ao movimento desse elétron é
Então, a nossa “espira” tem essa corrente e ela produz um campo magnético no centro desse círculo.
Passo 3
Beleza! Agora que temos a corrente associada ao elétron temos que calcular o campo produzido por essa corrente na posição do próton. Para isso, temos que usar Biot-Savart, já que não temos uma simetria cilíndrica ou coisa do tipo.
O campo produzido será
Como a corrente é circular em torno do próton, então que é constante e sai da integral.
Outra coisa também é que está sempre na direção radial e está tangente ao círculo então o produto vetorial entre esses dois é perpendicular ao círculo. Nós não estamos preocupados com a direção, então vamos nos atentar ao módulo de . Como é constante ele também sai da integral assim
Essa integral de nada mais é que o comprimento do círculo, ou seja, .
Substituindo o valor de
Resposta
Portanto, a letra d) é a resposta correta.