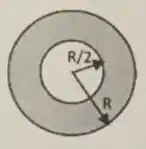
A densidade de corrente elétrica que passa num condutor é definida com o a corrente elétrica por unidade de área da seção transversal do condutor. Considere um cabo condutor cilíndrico oco muito longo de raio interno e raio externo , disposto ao longo do eixo , que transporta uma corrente no sentido (para fora do papel). A densidade de corrente na seção transversal é , onde é uma constante e é a distância radial do centro do condutor.
Utilizando a lei de Ampère:
- Determine o valor (módulo) do campo magnético no interior do cabo condutor, numa distância do centro.
- Determine o valor (módulo) do campo magnético no exterior do cabo condutor, para .
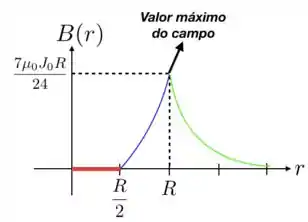
- Trace o gráfico do módulo do campo magnético em função da distância ao centro do cabo condutor. Indique no gráfico o valor máximo do campo magnético e o valor de para o qual isso acontece.
- Usando a lei de Ampère, determine o módulo do campo magnético total numa distância .
Considere agora que no centro do cabo (região oca) seja inserido um fio condutor de raio desprezível concêntrico ao cabo, que transporta uma corrente com sentido oposto ao da corrente anterior .
Passo 1
a) Como temos simetria cilíndrica, então, pela lei de Ampère, teremos
Como está saindo do plano da página, podemos colocar também saindo da página. Nesse caso, vamos ter
Passo 2
b) Para , vamos ter
Passo 3
c) Como para não há corrente, então o campo magnético será zero. Além disso, como , então o gráfico terá o seguinte comportamento
Passo 4
d) Para finalizar, para agora precisamos considerar também a corrente que está em . Essa corrente está no sentido, logo ela entra subtraindo! Portanto
A corrente total agora vai ser
Resolvendo Isso:
Show! Agora que já sabemos a corrente, vamos voltar para a lei de Ampere.
Como queremos saber o valor do campo na posição :
O sinal de menos indica que o sentido do campo agora é horário ao invés de anti-horário.
Resposta
- Olhar gráfico do Passo 3;