Um capacitor de placas paralelas e circulares está inicialmente descarregado. A partir de um certo instante, ele começa a ser carregado por uma corrente não estacionária. Durante tal processo de carga, considere as seguintes afirmativas: (I) o campo elétrico entre as placas é diferente de zero; (II) o campo magnético entre as placas é zero, e (III) o campo magnético fora das placas é diferente de zero. Indique a alternativa que registra qual(is) dessas afirmações é(são) correta(s).
- I
- II
- III
- I e II
- I e III
- II e III
- I, II e III
- Nenhuma
Passo 1
Analisando uma à uma: o campo elétrico entre as placas é diferente de zero;
Sim, para que o capacitor seja carregado precisa se criar um campo elétrico entre as placas. Pode pensar assim também: quando você carrega um elemento de circuito, você coloca uma diferença de potencial entre os terminais dele. Quando se cria uma ddp, automaticamente surge campo elétrico pela equação:
Passo 2
A segunda alternativa diz: o campo magnético entre as placas é zero;
Pela Lei de Ampère corrigida:
Podemos ver que a alternativa é falsa. Pois como existe uma corrente não estacionária, existe um campo elétrico não estacionário. Por conta disto o fluxo elétrico entre as placas do capacitor varia com o tempo:
Logo, segue que existe campo magnético.
Passo 3
A última alternativa diz: o campo magnético fora das placas é diferente de zero.
Esta alternativa é um pouco mais complicada, mas se analisarmos com calma... Quais ferramentas temos para determinar o campo magnético? A melhor delas é a Lei de Ampère, portanto podemos tentar rodar ela entre as placas do capacitor numa região fora delas;
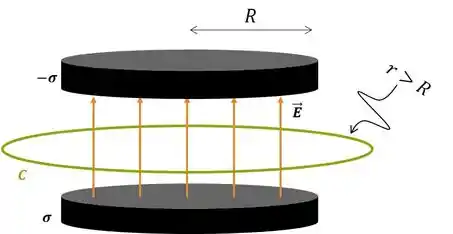
Aplicando a Lei corrigida, vemos que o fluxo de campo elétrico pela Amperiana não se anula e, pelo argumento do passo anterior, varia com o tempo:
Portanto:
Sim, existe campo magnético fora das placas. Afirmativa verdadeira.
Resposta
Letra e